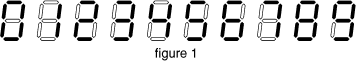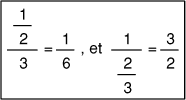9^e Championnat International des Jeux Mathématiques et Logiques
1/4 de finale individuels

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14.
• Catégorie GP (grand public): problèmes 5 à 14.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16.
• Catégorie HC (haute compétition): problèmes 5 à 16.

Énoncés des problèmes

Début catégorie CM

1 - Maya et ses soeurs (coefficient 1)

L'abeille Maya, représentée ci-dessous, et ses cinq soeurs, qui ont une forme identique, peuvent recouvrir entièrement la forme ci-contre, sans chevauchement.

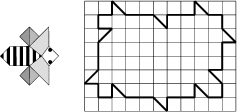
Dessinez le contour des six abeilles.

2 - Le voyage de Maya (coefficient 2)

Maya l'abeille se trouve sur un rayon de miel.

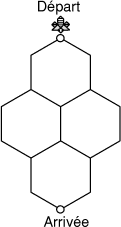
Elle se déplace sur le bord des alvéoles, et doit se rendre du point de départ au point d'arrivée (voir le dessin), par le chemin le plus court possible.
Combien existe-t-il de chemins différents possibles?

Début catégorie C1

3 - Des chiffres et des lettres (coefficient 3)

Français, Belges et Suisses comptent de la même manière jusqu'à soixante-neuf.
Quarante-huit a une curieuse propriété: la somme de ses chiffres 12 (= 4 + 8) est aussi le nombre de ses lettres.
Combien de nombres entiers (entre 1 et 69), y compris quarante-huit, ont un nombre de lettres égal à la somme de leurs chiffres?

4 - Les cinq poids (coefficient 4)

On dispose de cinq poids de 1 gramme, 2 grammes, 5 grammes, 6 grammes et 10 grammes.

Cochez toutes les masses comprises entre 1 et 24 grammes qu'on peut équilibrer en utilisant un ou plusieurs de ces cinq poids.

Début catégories C2 L1 GP L2 HC

5 - Le roudoudou de Doudou (coefficient 5)

Le petit Édouard sort de l'école et se précipite chez Madame Ladouceur, marchande de bonbons, juste en face de l'école. Il achète un bonbon (à 15 centimes) et tend une pièce de 1 F.
Désolé, mon petit, je n'ai pas de quoi te rendre la monnaie.
Doudou tend alors à la place une pièce de 50 centimes.
Je ne peux toujours pas te rendre la monnaie, et pourtant, il y a dans mon tiroir-caisse entre 50 centimes et 1 franc de monnaie, en pièces jaunes uniquement. Tu n'as pas une pièce de 20 centimes? Je pourrai te rendre la monnaie.
note: En France, les pièces jaunes sont les pièces de 5 centimes, de 10 centimes et de 20 centimes.
Combien y a-t-il de monnaie dans le tiroir-caisse de Madame Ladouceur?

6 - Le coup du menhir (coefficient 6)

Pour la fête d'Andromède, une de ses lointaines cousines, Obélix a taillé un énorme pavé de granit de 8 tonnes. Maintenant, il en taille un plus petit pour Galaxix, le chien d'Andromède: ses dimensions sont chacune le quart des dimensions du bloc précédent.
Combien pèse le bloc de Galaxix, en kilogrammes?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Le piège des matheux (coefficient 7)

Pierre, Irène, Emmanuel, Gilles et Évariste sont les cinq membres d'une famille de matheux; les phrases qu'ils prononcent sont toujours vraies ou fausses; voici cinq phrases soumises par ces joueurs rusés à votre perspicacité:

1. Pierre: PARIS s'écrit avec trois consonnes et deux voyelles.
2. Irène: Au Pays de Galles, le Mont Snowdon culmine à 1085 m.
3. Emmanuel: 2+3+5+7+11+13+17+19+23 = 100.
4. Gilles: La phrase prononcée par Irène est fausse.
5. Évariste: Une seule des phrases précédentes est vraie.

Parmi les cinq phrases ci-dessus, combien sont vraies?

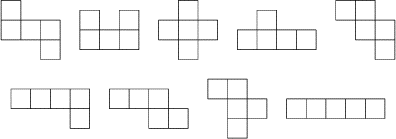
8 - Les pentaminos de Léon Tine (coefficient 8)

Léon Tine est un garagiste aussi efficace qu'astucieux. C'est pourquoi il a collé sur son enseigne les douze pentaminos dans un rectangle de 3 carreaux sur 20, ses initiales et un pentamino en forme de petite voiture stylisée ayant été préalablement coloriés en noir.

Placez les 9 pentaminos manquants représentés ci-dessous.
note: les pièces peuvent être tournées sur la face de votre choix.

9 - Troncadivisible (coefficient 9)

Si vous prenez le nombre 24 et que vous supprimez son chiffre des unités (4), vous obtenez 2, qui divise le nombre de départ 24. Un tel nombre, tel que, si on supprime son chiffre des unités, alors le nouveau nombre obtenu formé des chiffres restants, divise le nombre de départ, est dit troncadivisible.
Combien existe-t-il de nombres troncadivisibles inférieurs à 1995?

Fin catégorie C1

10 - La quadrichromie nette (coefficient 10)

Pour tester des nouveaux produits, Monsieur Lechat a besoin d'établir un plan d'expérimentations.
Schématisant chacun des quatre produits par une couleur, il réalise un cube 4×4×4 dans lequel tout alignement de quatre cubes (sauf en diagonale) comporte quatre couleurs (blanc, jaune, noir et vert).
Il vient juste de terminer son cube, mais il n'a pas encore eu le temps de terminer de noter le coloriage! Les V indiquent des faces vertes, et les J des faces jaunes.

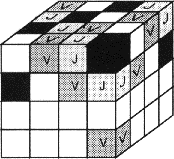
Sachant qu'immédiatement en dessous du cube vert du coin supérieur se trouve un cube blanc, pouvez-vous indiquer les couleurs des cubes se trouvant dans les étages 1 et 2 (l'étage 1 est celui du bas, et l'étage 2 celui immédiatement au-dessus)?

11 - La montre de Nicolas (coefficient 11)

Nicolas possède une montre à affichage digital. Chaque chiffre s'affiche grâce à un certain nombre de cristaux liquides (voir figure 1).

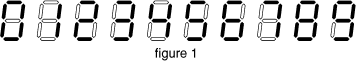
L'heure s'affiche de 0.00 à 23.59 (le chiffre des dizaines d'heures ne s'affiche que s'il est différent de 0; par contre, celui des dizaines de minutes s'affiche dans tous les cas). La partie gauche de la figure 2 montre, par exemple, l'affichage de 5 h 04, et celui de 17 h 04.

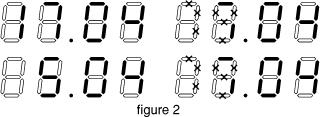
Si les cristaux liquides marqués d'une croix sur la partie droite de la figure 2 ne fonctionnaient plus, Nicolas ne pourrait plus distinguer l'affichage de 5 h 04 de celui de 17 h 04.
Quel nombre maximum de cristaux liquides (horizontaux ou obliques) peuvent ne plus fonctionner, sans qu'à aucun moment de la journée (de 0 h 00 à 23 h 59), il n'y ait ambiguïté sur la lecture de l'heure affichée, moyennant un petit effort de réflexion?

Fin catégorie C2

12 - Le numéro de code (coefficient 12)

Bernard et Francis se retrouvent devant chez Martine avec qui ils ont rendez-vous. Ils se demandent alors quel est le numéro de code de l'entrée de l'immeuble, que Martine leur a donné, mais qu'ils ont oublié de noter.
_ Je sais que le numéro de code est impair, qu'il comporte trois chiffres, et je me souviens de ces trois chiffres, dit Bernard. Il n'y a qu'à essayer toutes les combinaisons!
_ Attends, lui dit Francis, moi, je n'ai pas retenus les chiffres, mais j'avais remarqué que le nombre formé de ces trois chiffres est égal à 1 augmenté du triple du produit de deux nombres consécutifs. Cela peut sans doute t'aider!
_ Hélas, répond Bernard, cela ne réduit absolument pas le nombre de combinaisons à essayer. Heureusement, elles ne sont pas nombreuses!
Donnez, dans l'ordre croissant, les trois chiffres du numéro de code de l'entrée de l'immeuble où habite Martine.

13 - Une pile de fractions (coefficient 13)

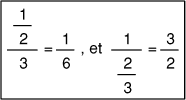
Les nombres 1, 2, et 3, empilés en fraction (voir encadré ci-contre) permettent d'obtenir deux résultats différents: 1/6 et 3/2, selon les priorités induites par la longueur des traits de fraction.
Combien de résultats différents peut-on obtenir, si l'on empile en fraction, dans cet ordre et de haut en bas, les nombres 1, 2, 3, 4, 5, 6, 7, et 8?

14 - Une opération volcanique (coefficient 14)

Lors de la dernière éruption de ce volcan, nous avons pu observer les coulées de LAVE et de MAGMA qui se divisaient à n'en plus finir. Rien ne semblait pouvoir arrêter leur progression vers la VALLEE.

  L A V E
-----------  =  0,VALLEEVALLEEVALLEE...
 M A G M A

Comme dans tout cryptarithme, deux lettres différentes remplacent toujours deux chiffres différents, et deux chiffres différents sont toujours remplacés par deux lettres différentes. Le 0 du quotient représente le chiffre zéro, mais d'autres zéros peuvent être remplacés par une lettre.
Que vaut VALLEE?

Fin catégories L1 GP

15 - Les feux rouges (coefficient 15)

Frédéric, qui se veut mathématicien, simule sur ordinateur la circulation routière dans la rue principale de sa ville. On suppose que dans cette avenue, il y a n feux numérotés de 1 à n (n > 0), et qu'à un instant donné, chaque feu est soit rouge, soit orange, soit vert. Pour optimiser le trafic, Frédéric affirme qu'il faut remplir la condition suivante:
quels que soient p et q distincts, si les feux numéros p et q sont de la même couleur, alors le feu numéroté p+q n'est pas de cette couleur.
Que vaut n, au maximum?

16 - Le théorème discret (coefficient 16)

Dans l'espace discret, c'est-à-dire dont tous les points sont à coordonnées entières, Francis prétend avoir trouvé le nombre n minimum de points différents qu'il faut choisir pour être certain que parmi tous les triangles formés par ces points, il y en a au moins un dont les coordonnées du centre de gravité seront entières!
Quel est le nombre de Francis?

Fin catégories L2 HC