10^e Championnat International des Jeux Mathématiques et Logiques
finale internationale, 1^re séance, 30 août 1996

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Les 7 pièces (coefficient 1)

Je dispose de 7 pièces de monnaie alignées, toutes tournées du côté pile. J'ai le droit de retourner d'un seul coup deux pièces placées côte à côte.

Combien de coups faut-il, au minimum, pour que deux pièces voisines soient toujours sur des côtés différents (pile-face ou face-pile)?
Attention, 1 coup consiste à retourner 2 pièces.

2 - Un petit tour de vélo (coefficient 2)

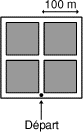
Mathias a fait un pari avec Mathilde. Son pari consiste à faire, en vélo, le trajet le plus long possible dans le quartier représenté ci-contre, en respectant les conditions suivantes:
Mathias peut passer plusieurs fois par le même carrefour, mais il ne doit pas emprunter plus d'une fois la même rue. Lorsqu'il ne peut plus respecter ces conditions, il revient alors en marchant.
Donnez la longueur, en hectomètres, du trajet de Mathias en vélo.
(On ne tient pas compte de la largeur des rues).

Début catégorie C1

3 - La carte d'Adrien (coefficient 3)

Adrien a colorié la carte d'un continent imaginaire. Au centre de ce continent est situé un lac autour duquel sont répartis quatorze pays comme indiqué sur le dessin.

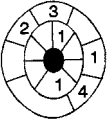
Les nombres 1, 2, 3, 4 représentent quatre couleurs différentes, et on sait qu'Adrien a utilisé: trois fois la couleur 1, trois fois la couleur 2, quatre fois la couleur 3, quatre fois la couleur 4. De plus, deux pays voisins sont toujours de couleurs différentes.
Donnez un coloriage de la carte d'Adrien.

4 - Six dans un rectangle (coefficient 4)

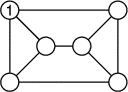
Dans les cercles du rectangle ci-dessous, placez les nombres de 2 à 6 (le 1 est déjà placé). La différence entre deux nombres directement reliés par un segment doit toujours être plus grande que 1.

Début catégories C2 L1 L2 GP HC

5 - Le tableau incomplet (coefficient 5)

Voici un tableau d'addition à compléter (par exemple, A + H = 15).
On sait que la somme de tous les nombres écrits dans le carré entouré en gras est égale à 200.

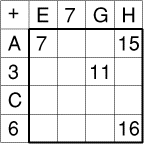
Trouvez les nombres écrits dans la ligne C.

6 - 4 pas en avant, et 3 en arrière (coefficient 6)

En partant de A, qui est une voyelle, j'avance de 4 lettres dans le sens de la flèche, et j'arrive à la lettre E, qui est également une voyelle. Je continue ensuite selon le principe suivant:

• si la lettre sur laquelle je suis arrivé est une voyelle, j'avance de 4 lettres dans le sens de la flèche,
• si cette lettre est une consonne, alors je recule de 3 lettres.

En partant de A, qui est ma première lettre, et en continuant selon la règle expliquée plus haut, quelle sera ma 96^e lettre?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Les cèdres du père Fectionniste (coefficient 7)

Dans la propriété de Monsieur Fectionniste, que l'on peut représenter par un carré quadrillé de 5 carreaux sur 5, se trouvent cinq magnifiques cèdres du Liban.

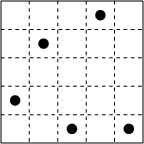
Ayant 4 filles très jalouses les unes des autres, il veut partager sa propriété en respectant les conditions suivantes:

• la propriété est partagée en 5 parties de même aire,
• chacune des filles a une partie possédant un cèdre,
• les formes des propriétés des 4 soeurs sont superposables (par glissement ou par retournement),
• M. Fectionniste garde un terrain de forme différente avec un cèdre, et touchant (par un côté) le terrain de chacune de ses filles,
• la propriété de chacune des filles touche (par un côté) les propriétés de deux de ses soeurs exactement.

Aidez ce brave homme à faire un plan correspondant à tous ces souhaits.

8 - Les années carrément chiffrables (coefficient 8)

On appelle carré parfait un nombre égal au produit d'un autre nombre par lui-même, comme par exemple 0 = 0 × 0, 1 = 1 × 1, 4 = 2 × 2, 9 = 3 × 3, 16 = 4 × 4, ...
1996 est une année parfaitement chiffrable, car la somme de ses chiffres est un carré parfait. En effet, 1 + 9 + 9 + 6 = 25, qui est le carré de 5.
Combien y a-t-il d'autres années parfaitement chiffrables durant tout le 20^e siècle?

9 - Un peu de logique (coefficient 9)

René affirme ce qui suit:

1. des trois propositions A, B et C, une seule est vraie,
2. des trois propositions B, C et D, une seule est vraie,
3. des propositions A et D, une seule est vraie!

D'autre part, Andrée prétend ceci:

1. de A, B et C, une seule proposition est vraie,
2. de B, C et D, une seule proposition est vraie,
3. de A, C et D, une seule proposition est vraie!

Un des deux personnages ment au moins une fois (l'autre dit la vérité).
Sur le bulletin-réponse, entourez les propositions vraies.

Fin catégorie C1

10 - La T.G.E. (coefficient 10)

La Très Grande Échelle possède une infinité de barreaux régulièrement espacés. Gilles Grimpé escalade l'échelle par séries de 13 barreaux. Après avoir grimpé chaque série de 13 barreaux, G. Grimpé souffle un peu pour reprendre des forces. Mais, pendant qu'il souffle, fatigué, après la première série de 13 barreaux, il redescend d'un barreau, après la seconde série de 13 barreaux, il redescend de deux barreaux, après la troisième, il redescend de trois barreaux, et ainsi de suite, la fatigue augmentant...
Après combien d'escalades de 13 barreaux Gilles sera-t-il revenu au niveau du sol?
Répondez 0 si vous pensez qu'il ne redescendra jamais au niveau du sol.

11 - Les voisines donnent le score (coefficient 11)

Jean-Philippe, excellent joueur de tennis de table, a trouvé un moyen pour indiquer le score obtenu par ses adversaires, souvent infortunés. Six balles de tennis de table sont disposées en cercle (voir le dessin).

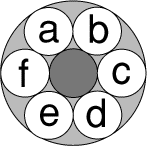
Sur chaque balle est inscrit un nombre différent: 1, 2, 3, 4, 5, ou 6. À la fin de la partie, Jean-Philippe prononce une série de nombres, inscrits sur des balles voisines, la somme de ces nombres donnant le score de son adversaire.
Les balles voisines peuvent être au nombre de six, de cinq, de quatre, de trois, de deux, ou bien il peut s'agir d'une seule balle.
Tous les scores de 1 à 21 peuvent être atteints, et l'on sait que a = 1, que b < f, et que deux nombres consécutifs ne sont jamais inscrits sur deux balles immédiatement voisines (comme par exemple d et e).
Trouvez la disposition des balles de Jean-Philippe.

Fin catégorie C2

12 - L'année faste (coefficient 12)

L'année faste fut une année historique postérieure à l'an mil, c'est-à-dire que son millésime comptait quatre chiffres.
Si l'on sépare les deux premiers chiffres et les deux derniers chiffres du millésime de l'année faste, on obtient deux nombres à deux chiffres. Chose extraordinaire, le double produit de ces deux nombres à deux chiffres est égal au millésime lui-même.
Retrouvez ce millésime.

13 - Le professeur est un rêveur... (coefficient 13)

José avait demandé à ses élèves de découper un parallélogramme dans une feuille de carton: Je veux qu'il ait une hauteur de 7 cm, un côté de 14 cm et une diagonale de 37 cm, avait-il dit.
Au cours suivant, il fut très surpris de constater que quatre de ses élèves ont trouvé des dessins différents correspondant à sa demande. Julie et Annabel, qui avaient des parallélogrammes différents, mais de même aire, Vincent et Julien. José fut troublé lorsque Vincent lui annonça que son parallélogramme avait une aire double de celle du parallélogramme de Julien!
Voyons cela dit-il...
Aux erreurs de mesure près, cela semble exact, mais cela ne l'est pas tout-à-fait... En tout cas, bravo pour votre sens de l'observation.
Quelle valeur conviendrait pour la longueur de la diagonale pour que, sans changer les autres dimensions, parmi les quatre solutions, la solution de Vincent ait une aire exactement double de celle de Julien? Vous donnerez la valeur exacte en utilisant éventuellement des radicaux.

14 - La planète des jeux (coefficient 14)

C'est un monde ludique et idyllique. Bien sûr, parmi ses 12 000 habitants, il y a ceux qui préfèrent les jeux de cartes, il y a les fadas du jeu d'échecs, les mordus des jeux de rôle, etc... mais tout le monde joue à tout, et l'harmonie (il y a aussi les joueurs de piano) règne dans cette civilisation.
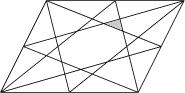
Le drapeau de la planète des jeux, qui a la forme d'un parallélogramme, reflète bien la répartition selon les préférences de chacun: chaque région du drapeau représente un type de jeux, son aire étant proportionnelle au nombre des pratiquants de ce type de jeux. La région grisée représente les amateurs de jeux mathématiques. Combien y a-t-il de ces derniers?
note: les sommets du polygone étoilé sont les sommets du parallélogramme et les milieux des côtés.

Fin catégories L1 GP

15 - Les 9 facteurs revisités (coefficient 15)

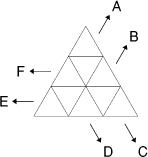
Tous les nombres entiers de 1 à 9 ont été disposés dans les neuf cases triangulaires du dessin ci-contre. On a ajouté un signe - devant certains d'entre eux.
Les lettres A, B, C, D, E et F représentent les produits, dans une direction donnée, de trois ou cinq de ces nombres.
On donne:

A	B	C	D	E	F
320	162	6048	-60	756	-240

Retrouvez les neuf nombres.

16 - Le terrain du père Cussion (coefficient 16)

Xavier-Édouard Cussion vient d'acheter pour sa fille Gladys, un terrain en forme de pentagone non régulier. Gladys n'a pas encore vu le terrain, mais elle connaît déjà les éléments suivants:

• le pentagone est constitué de 2 petits côtés mesurant tous les deux 20 mètres de long, et de 3 grands côtés, eux aussi de même longueur,
• les deux petits côtés sont consécutifs et forment un angle droit à l'intérieur du terrain,
• le grand côté non adjacent à un petit côté est parallèle à un des deux petits côtés,
• aucun angle entre deux grands côtés n'est obtus.

Quelle est l'aire minimum du terrain de Gladys et X.-E. Cussion? Donner la réponse arrondie au m² le plus proche (on prendra 1,414 pour √2).

Fin catégories L2 HC