11^e Championnat International des Jeux Mathématiques et Logiques
finale internationale, 1^re séance, 29 août 1997

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Combinaison (coefficient 1)

Mathias et Mathilde sont poursuivis par de féroces antimaths. Ils arrivent devant une énorme porte blindée à ouverture codée. Il faut faire vite!
Mathias se souvient qu'il a dérobé le porte-clef d'un chef antimath. Ce porte-clef est constitué d'un prisme à trois faces rectangulaires, sur chacune desquelles se trouvent gravés des signes bizarres.

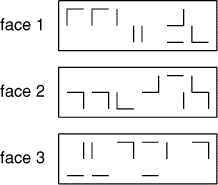
Mathilde s'exclame: heureusement que nous avons ce porte-clef, regarde!
... Et ils purent ouvrir la porte.
Quelle était la combinaison du code?

2 - Les petits caméléons (coefficient 2)

Dans le pays de Noiréblanc, les caméléons ont de drôles d'habitudes. Le corps des jeunes caméléons est constitué de trois cases qui peuvent être noires ou blanches, et passer d'une couleur à l'autre selon les circonstances. Lorsque deux caméléons se croisent, les cases en contact changent de couleur suivant la règle illustrée sur le dessin ci-contre.

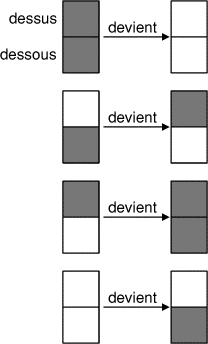
Deux caméléons se rencontrent et l'un passe par-dessus l'autre. Voici leur position et leurs couleurs au départ:

On demande de colorier la position finale.

Début catégorie C1

3 - Dominos à replacer (coefficient 3)

Quatre dominos ont été placés ainsi pour représenter une multiplication juste.

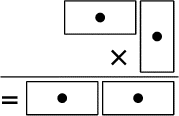
Voici les dominos employés.

Replacez-les.

4 - Le chêne et le cerisier (coefficient 4)

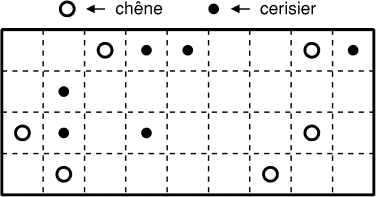
Monsieur Plexe est un homme heureux: il possède un beau terrain planté de chênes et de cerisiers. M. Plexe est également père de six enfants. Il a cependant un petit problème de partage: il veut en effet léguer à chacun de ses enfants une portion de son terrain ayant la même aire, la même forme, et contenant un chêne et un cerisier. Pouvez-vous aider le père Plexe (on suivra les lignes du quadrillage)?

Début catégories C2 L1 L2 GP HC

5 - La boîte à couverts (coefficient 5)

Cette boîte à couverts présente quatre compartiments de mêmes dimensions.
Le périmètre de cette boîte étant de 112 cm, quelle est son aire (en cm²)?

6 - Deux allumettes voyageuses (coefficient 6)

Neuf allumettes, désignées par les lettres a, b, c, d, e, f, g, h et i sont placées comme sur le dessin.

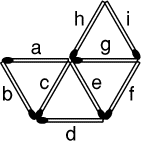
Sur cette figure, on compte quatre petits triangles équilatéraux. Il faut déplacer deux allumettes seulement et les repositionner pour qu'il ne reste que trois petits triangles équilatéraux. Les neuf allumettes doivent alors toutes être un côté d'un triangle, et on ne peut pas superposer deux allumettes.
Adrien prétend qu'il existe six solutions différentes à ce problème. Retrouvez-les en notant le nom des allumettes déplacées.

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Le nombre de José (coefficient 7)

José, qui adore jouer avec les nombres, choisit un nombre à deux chiffres. Il calcule successivement la somme des deux chiffres, leur produit et leur différence (le plus grand moins le plus petit), puis additionne les trois résultats. Stupeur! Le total est égal au nombre de départ!
Quel était le nombre choisi par José?

8 - Les grands caméléons (coefficient 8)

Dans le pays de Noiréblanc, les caméléons ont de drôles d'habitudes. Le corps des caméléons adultes est constitué de sept cases qui peuvent être noires ou blanches, et passer d'une couleur à l'autre selon les circonstances.
Lorsque deux caméléons se croisent, les cases en contact changent de couleur suivant la règle illustrée sur le dessin ci-contre.

Deux caméléons se rencontrent et l'un passe par-dessus l'autre. Voici leur position et leurs couleurs au départ:

On demande de colorier la position finale.

9 - Les hexiamants (coefficient 9)

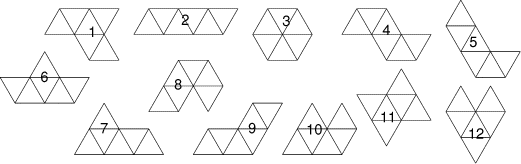
Ci-dessus sont représentées 12 hexiamants (formes obtenues en réunissant 6 triangles équilatéraux). Avec 8 d'entre elles, on peut remplir l'étoile ci-contre. La pièce n° 8 a déjà été placée.

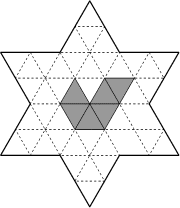
Placez les autres, en les faisant glisser, mais écrivez sur le bulletin-réponse les numéros des formes qui ne servent pas.

Fin catégorie C1

10 - Frugalement votre (coefficient 10)

Francis vient d'acquérir un verger carré de 2116 m², délimité aux quatre sommets, dans cet ordre, par un abricotier, un bananier, un citronnier, et un dattier.
Sur les bords du terrain se trouvent un figuier et un goyavier, le figuier étant situé entre l'abricotier et le bananier et le goyavier entre l'abricotier et le dattier. La distance abricotier-goyavier est de 20 mètres alors que la distance abricotier-figuier est de 21 mètres.
Une allée est tracée, reliant en ligne droite le figuier au goyavier. Une seconde allée, perpendiculaire à la première, passe par le citronnier. Ces deux allées se croisent au pied d'un magnifique épicéa.
Quelle est la distance, arrondie au décimètre le plus proche, entre l'épicéa et le citronnier?

11 - Les 3 polygones (coefficient 11)

Trois polygones ont à eux trois 97 diagonales.
Combien ont-ils de côtés, à eux trois?

Fin catégorie C2

12 - Travaux manuels (coefficient 12)

Dans une classe de collège, le professeur de mathématiques donne à chaque groupe de deux élèves une feuille de carton rectangulaire. Chaque groupe partage son rectangle en deux suivant une diagonale. Le professeur demande à chacun de mesurer le périmètre de son triangle rectangle, ce qui est facilement fait. Ensuite, la consigne est que chacun découpe son triangle en 2 ou 3 morceaux, chaque coupe étant rectiligne, pour former un quadrilatère avec les morceaux obtenus, et de mesurer le périmètre de celui-ci.
Dans le groupe formé par Mathias et Mathilde, Mathias a obtenu un losange, et Mathilde un rectangle. On constate alors que le périmètre du triangle rectangle de départ surpasse de 8 cm celui du losange, et que celui du losange surpasse de 8 cm celui du rectangle.
Quelle est l'aire du rectangle en carton donné par le professeur? On donnera la réponse en cm².

13 - Mini-liaisons additives (coefficient 13)

Soit un graphe dont chaque noeud comporte un entier. Faisons correspondre à cet entier la somme de tous ses voisins. Par exemple (figure ci-contre):

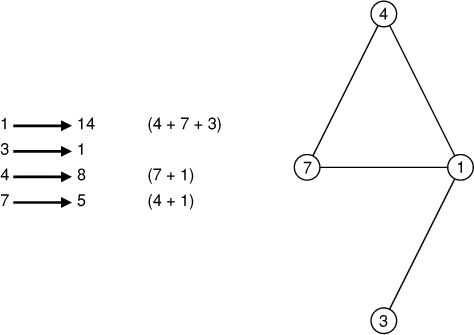
Francis a établi les correspondances d'un graphe comportant tous les entiers de 0 à 9, il a écrit ces correspondances, mais hélas les nombres des noeuds ont été effacés...
Pouvez-vous reconstituer le graphe?

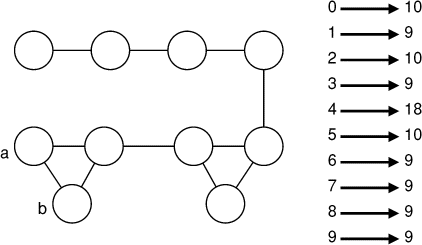
(a < b)

14 - Drôles de machines (coefficient 14)

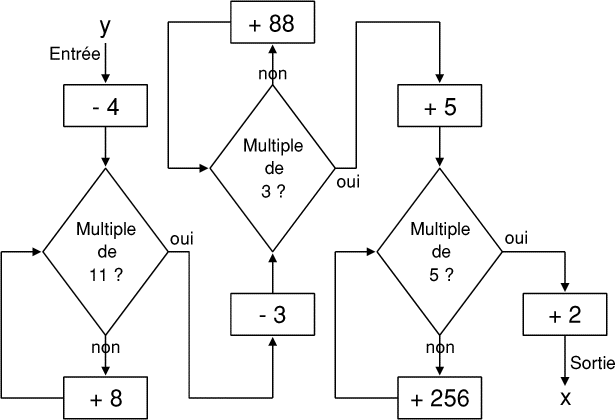
Mathias a apporté trois machines à fabriquer des nombres. Il les a mises en série comme sur le dessin ci-dessus.
Francis demande à Mathias combien de valeurs de y vont donner 3997 à la sortie. Donnez en deux.

Fin catégories L1 GP

15 - Désintégration de l'atome (coefficient 15)

Un atome occupe une position d'abscisse entière x, telle que 2 < x < 48, sur une cible rectiligne graduée de 0 à 50. On se propose de l'atteindre avec un proton dont on peut choisir, sur la cible, le point d'impact d'abscisse entière comprise (au sens large) entre 0 et 50.
Si cette abscisse est égale à celle de l'atome, celui-ci est désintégré. Sinon, il est repoussé à une distance d' = E(49/d), où E désigne la partie entière et d la distance qui séparait l'atome du point d'impact.
Par exemple, si l'atome a pour abscisse 21, un tir sur 18 le ferait passer à l'abscisse 21 + E(49/(21-18)) = 37.
Toujours si l'atome a pour abscisse 21, un tir sur 30 le ferait passer à 21 - E(49/(30-21)) = 16.
Trouver une succession de tirs, la plus courte possible, telle que quelle que soit l'abscisse initiale inconnue x de l'atome, le dernier tir désintègre l'atome.
note: Si l'atome est repoussé hors des limites de la cible, il est alors considéré comme perdu, mais n'est pas désintégré comme on le souhaite.

16 - Les vaches de John (coefficient 16)

John Beef est un paisible éleveur, père de trois enfants d'âges tous différents. Si vous demandez à John le nombre de têtes de bétail de son cheptel, il vous répondra d'une façon sibylline:
Si je multiplie le nombre de mes bêtes par le produit des âges de mes trois enfants, j'obtiens le même résultat que si j'ajoute au carré du nombre de bêtes de mon troupeau la somme des carrés des âges de mes enfants. De plus, le nombre de têtes de bétail de mon troupeau est bien supérieur à l'âge de ma fille aînée, mais ce nombre est le plus petit possible permettant cette égalité avec quatre nombres tous différents.
Combien John Beef possède-t-il d'animaux?
note: Le troupeau de John, constitué de bovins, est certifié parfaitement sain sur le plan vétérinaire.

Fin catégories L2 HC