11^e Championnat International des Jeux Mathématiques et Logiques
finale internationale, 2^e séance, 30 août 1997

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Podium pour marathon (coefficient 1)

Avec 10 pièces de la forme suivante:

on veut remplir le podium à neuf places.

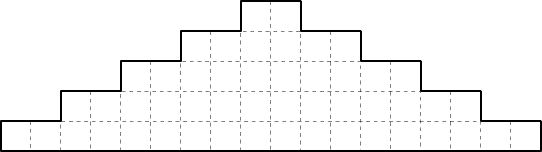
Dessinez le contour des dix formes.
note: les formes peuvent être retournées.

2 - Les huit nombres (coefficient 2)

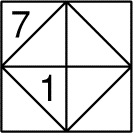
On veut remplir les huit cases triangulaires de cette grille avec les nombres de 1 à 8. La différence entre les nombres de deux cases adjacentes par un côté doit toujours être au moins égale à 3. Les nombres 1 et 7 sont déjà placés.
Complétez les cases vides.

Début catégorie C1

3 - Des papés sur un banc (coefficient 3)

Sur la grand'place de leur village provençal, quatre papés bavards: Arsène, Ernest, Isidore et Oscar, sont assis côte à côte sur un banc, à l'ombre.
Ils ne se sont pas placés au hasard. Ainsi, Ernest ne voisine pas avec Arsène ou Isidore, qui ne sont pas ses meilleurs amis. Isidore ne côtoie pas Oscar, car celui-ci mange trop d'ail. Ernest, quant à lui, n'a personne à sa gauche, car il est sourd de l'oreille gauche.
Quelle est la disposition la plus logique des anciens sur leur planche?
répondez en citant les initiales des 4 papés, dans l'ordre, tels que vous les voyez, face à vous.

4 - Labyrinthe numérique (coefficient 4)

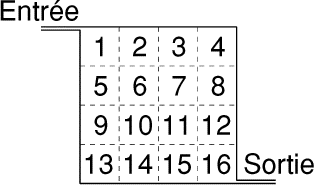
Dans ce labyrinthe, on additionne les points des cases que l'on traverse. On ne peut passer d'une case à une autre que si elles se touchent par un côté, et on ne doit jamais passer deux fois ou plus de deux fois sur une même case.
Quel est le plus grand total que l'on puisse atteindre en traversant ce labyrinthe?

Début catégories C2 L1 L2 GP HC

5 - Les ailes du destin (coefficient 5)

Le petit Kevin a toujours peur de se tromper, aussi a-t-il toujours avec lui une table de multiplication.

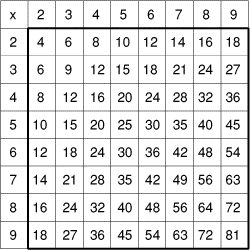
Son frère Mathias aime lui poser des énigmes. Il a fabriqué en fil de fer deux petits L identiques, qu'il peut poser sur la table de multiplication en les orientant de huit façons possibles.

Mathias a disposé, avec l'orientation du dessin ci-dessus, les deux L sur la table de multiplication, et a fait la somme des quatre nombres inscrits dans chaque L. Il a trouvé 153 et 162. Kevin doit retrouver la place de ces deux L, qui peuvent se toucher, mais sans qu'il y ait recouvrement.
Aide Kevin!

6 - Cinq pour un (coefficient 6)

Nina doit reconstituer un puzzle: quatre pièces pour former un carré. Facile! Mais voilà qu'une pièce d'un autre puzzle est venue se mélanger avec les quatre pièces. Nina se trouve donc en présence de cinq pièces, et elle a oublié comment était agencé le carré. Aidez-la à reconstituer le carré!

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Le tableau de l'année (coefficient 7)

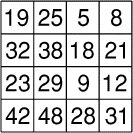
Adrien a fabriqué un tableau de nombres dont il est fier. Il propose donc à Thomas de choisir quatre nombres tels que deux d'entre eux ne soient jamais sur une même ligne ni sur une même colonne. Thomas s'exécute. Calcule leur somme demande Adrien. C'est curieux dit Thomas. Recommence avec un autre groupe de quatre nombres, ajoute Adrien. Tiens, tiens, ..., dit Thomas.
Ce tableau n'est pas le fruit du hasard, observez-le bien! Thomas, ne voulant pas être en reste, a lui aussi construit un tableau ayant la même propriété, et la même somme que celui d'Adrien. Malheureusement, certains nombres ont été effacés. Reconstituez-le.

8 - Les 11 amis et la galette (coefficient 8)

Un groupe de 11 amis, Messieurs Zéro, Quatre, Cinq, Six, Sept, Huit, Neuf, Dix, Onze, Douze et Treize, se retrouvent autour d'une galette (Messieurs Un, Deux et Trois ne pouvaient venir et se sont excusés).
M. Zéro est au régime; il ne mange donc pas de galette, mais il coupe les parts pour ses amis. Il donne 1 / 4 de la galette à M. Quatre, 1 / 5 de la galette à M. Cinq, 1 / 6 de la galette à M. Six, etc..., en continuant dans l'ordre, et en augmentant à chaque fois le dénominateur d'une unité, en concordance avec le nom de la personne servie.
M. Zéro, qui est nul en calcul, s'aperçoit subitement, quand vient le tour d'un de ses 10 amis, qu'il ne reste que des miettes et qu'il ne peut servir cet ami en suivant la règle qu'il s'est fixée.
Donnez le nom de cet ami de M. Zéro.

9 - Les cartes de Mickaelus (coefficient 9)

Les cartes de Mickaelus sont au nombre de seize. Au recto, elles portent les nombres de 1 à 16 écrits en chiffres arabes. Au verso, elles portent les nombres de 1 à 16 écrits en chiffres romains. Mais les nombres du recto et du verso ne se correspondent pas forcément.

On sait que:

• à un nombre de 2 lettres en chiffres romains correspond un nombre multiple de 2 en chiffres arabes
• à un nombre de 3 lettres en chiffres romains correspond un nombre multiple de 3 en chiffres arabes.

Combien y a-t-il, au maximum, de cartes qui portent le même nombre au recto et au verso?

Fin catégorie C1

10 - Véritablement timbrés (coefficient 10)

Bernard, Michel et Francis collectionnent des timbres à la gloire de la F.F.J.M. Chacun essaie de les disposer en rangées de 17 timbres; hélas, il reste 8 timbres non rangés à chacun! Bernard propose alors de faire des rangées de 19 timbres; chose curieuse, il reste encore 8 timbres non rangés à chacun des collectionneurs!
Les trois amis possèdent chacun plus de 1000 timbres, mais moins de 2000, et les effectifs de leurs collections sont tous différents.
Combien de timbres possèdent-ils à eux trois?

11 - Jogging forestier (coefficient 11)

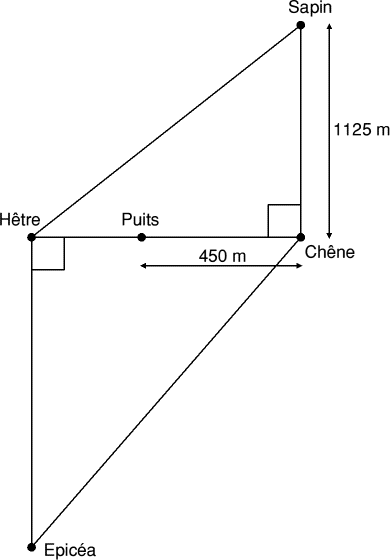
Fabien se trouve près du vieux puits.

• Il sait que le parcours Puits-Chêne-Sapin a exactement la même longueur que le parcours Puits-Hêtre-Sapin.
• En revanche, le parcours Puits-Chêne-Epicéa fait 300 m de plus que le parcours Puits-Hêtre-Epicéa.
• Fabien se décide à courir jusqu'au chêne, à faire, toujours en courant deux grands tours chêne-sapin-hêtre-épicéa-chêne, et enfin à revenir au puits où il a laissé des affaires.
• Fabien court régulièrement à 10 km par heure.
• Fabien est parti du puits à 8 heures précises du matin.

À quelle heure précise reviendra-t-il au puits?

Fin catégorie C2

12 - Le vélo de consolation (coefficient 12)

Afin de se consoler de ne pas partir en vacances, Pierre et Paul viennent de mettre en commun leurs économies (d'un montant inférieur à 1000 F) pour acheter un vélo.
Curieux, se dit Pierre, Le montant de la part que j'ai payée s'écrit avec les mêmes chiffres que le prix du vélo, mais en ordre inverse.
Encore plus curieux, dit Paul, Le montant de ma part s'écrit encore avec les mêmes chiffres, mais dans un ordre encore différent.
Quel est le prix du vélo?

13 - La poignée de l'outil mystérieux (coefficient 13)

Cet outil mystérieux, que l'on peut considérer comme plat, présente un axe de symétrie vertical et comprend une poignée, un corps et deux pieds, dont toutes les dimensions sont des nombres entiers de centimètres strictement positifs. Le dessin ci-après en respecte la forme générale, mais pas les proportions. Deux outils identiques peuvent s'assembler parfaitement de deux façons représentées en (1) et (2).

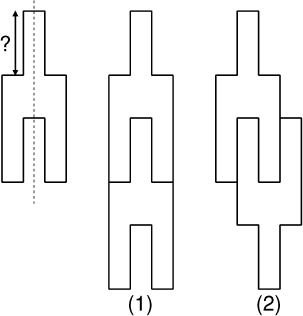
L'assemblage (1) a un périmètre de 2,60 m, tandis que celui de l'assemblage (2) est seulement égal à 2,28 m.
Quelle est la longueur de la poignée?

14 - La noix de son maître (coefficient 14)

La chienne Hexane aime les noix, mais elle ne peut les casser!
Aussi, elle doit les rapporter à son maître pour que celui-ci réalise cette opération à sa place. Entre le maître et l'animal, la règle du jeu est relativement simple. Le maître divise le tas de noix en deux parties égales, et il garde l'une des deux parties. Ce faisant, s'il reste une noix, elle est pour Hexane. On continue ainsi l'opération avec l'autre partie, jusqu'à ce qu'il ne reste plus de noix.
Par exemple, si Hexane rapporte 1903 noix, les tas successifs compteront 951, 475, 237, 118, 59, 29, 14, 7, 3 et 1 noix. Et Hexane aura pu en manger neuf.
Hexane ne peut rapporter plus de 1998 noix.
Combien doit-elle en rapporter afin de pouvoir en déguster le maximum?

Fin catégories L1 GP

15 - Sûr de gagner (coefficient 15)

Richard possède un nombre illimité de billes (son père en fabrique). Il a inventé le jeu suivant. Il donne un nombre impair de billes à son petit frère. Ce dernier doit alors partager le tas de billes en deux tas dont les effectifs sont des nombres composés premiers entre eux. S'il réussit, le petit frère a gagné. Dans le cas contraire, c'est Richard le gagnant.
Richard a repéré des nombres qui lui permettent de gagner à coup sûr. On appelle ces nombres des nombres de Richard.
Quel est le plus grand nombre (impair) de Richard?
Répondez 0 si vous pensez qu'un tel nombre n'existe pas.

16 - Carré moyen (coefficient 16)

Soit un carré de 15 m de côté, quadrillé par des lignes parallèles à ses côtés, tracées tous les millimètres.
Quelle est l'aire moyenne de tous les carrés qui ont leurs sommets situés aux noeuds du quadrillage?
Donnez une réponse approchée, arrondie au m².

Fin catégories L2 HC