12^e Championnat International des Jeux Mathématiques et Logiques
demi-finale, 14 mars 1998

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Annales plus (coefficient 1)

Les nouvelles annales du Championnat comportent 96 pages. Trois volumes paraissent tous les deux ans, les trois premiers ayant paru en 1997. En quelle année dépassera-t-on 1998 pages?

2 - Sur la route de Roiché (coefficient 2)

Michel, qui rentre chez lui et roule vers Roiché (et vers Fortal), vient de dépasser le panneau ci-contre.

Quelque temps plus tard, il passe devant un autre panneau portant les deux indications suivantes:

  FORTAL  ..   ROICHÉ  .,.

Il remarque alors que les deux distances, exprimées en kilomètres, sont écrites à l'aide des mêmes chiffres, dans le même ordre, et ne diffèrent que par l'existence d'une virgule dans la seconde.
À quelle distance Michel se trouve-t-il alors de Roiché?

Début catégorie C1

3 - La course d'Hexane (coefficient 3)

Lors d'une randonnée en ligne droite, Gilles a 1998 mètres d'avance sur Hexane. Or, en une seconde, Hexane parcourt 5 mètres, tandis que Gilles n'en parcourt que 2.
Dans combien de secondes la chienne aura-t-elle rattrapé le maître?

4 - Le dé tétraédrique (coefficient 4)

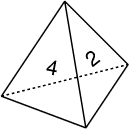
Ce dé possède 4 faces identiques (non transparentes) numérotées de 1 à 4.
On le pose sur sa face 1, sur la case a d'un hexagone (voir la figure ci-dessous, vue du dessus), puis on fait basculer le dé autour d'une de ses arêtes, de façon à l'amener successivement en b, en c, en d, en e, puis en f.

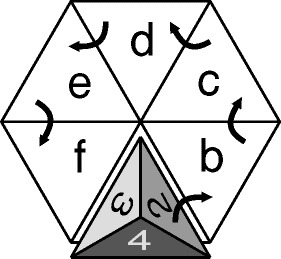
Sur quelle face repose-t-il alors?

Début catégories C2 L1 L2 GP HC

5 - Les sept pièces (coefficient 5)

Sept pièces de monnaie sont alignées, toutes tournées du côté pile. À chaque coup, on peut retourner simultanément trois pièces de son choix.
Quel est le nombre minimum de coups nécessaires pour que les sept pièces soient toutes tournées du côté face?

6 - À l'envers (coefficient 6)

  . . . . . . . . × . = 98765432

Le premier membre de l'égalité ci-dessus comporte deux facteurs où chaque chiffre de 1 à 9 apparaît une fois. Pourtant, il ne s'agit pas de la solution facile 98765432 × 1 = 98765432.
Que vaut le second facteur?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - L'étage de José (coefficient 7)

José habite au 4^ème étage d'un immeuble, dans l'appartement numéro 49. Dans cet immeuble, les appartements sont numérotés à partir de 1, dans l'ordre, étage par étage en partant du rez-de-chaussée. Tous les étages, y compris le rez-de-chaussée, comptent le même nombre d'appartements.
Tous les appartements de l'étage de José sont occupés par des célibataires sans enfant. Combien José a-t-il de voisins à son étage?

8 - Un segment et des carrés (coefficient 8)

36 clous sont plantés régulièrement comme sur la figure ci-contre.

On veut tendre une ficelle pour former un carré qui entoure le segment noir. Ce segment ne doit toucher aucun côté du carré, mais un côté du carré peut toucher deux ou plusieurs autres clous.
Combien de carrés différents répondant à ces conditions peut-on construire?

9 - Le gros lot (coefficient 9)

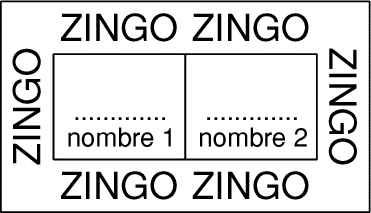
En Syldavie, il existe un jeu de hasard très populaire appelé le zingo. Pour jouer, il faut décider d'une mise égale au maximum à 20 couronnes syldaves, et partager cette mise, exprimée en couronnes, en deux nombres entiers que l'on inscrit sur le bulletin de jeu. Si le bulletin est gagnant, l'heureux joueur reçoit alors une somme égale au produit du carré du premier nombre par le cube du second (on rappelle que le carré de 5, par exemple, est 5×5, et que son cube est 5×5×5). Quel gain maximum peut-on espérer pour un bulletin de zingo?

Fin catégorie C1

10 - L'île fleurie (coefficient 10)

L'île fleurie est ainsi nommée car, à la belle saison, ses nombreux arbres fruitiers sont en fleurs, et que cela est joli à voir. Ces arbres sont disposés de telle sorte qu'il y ait en moyenne un arbre pour 18 m² de terrain. L'île a la forme d'un rectangle deux fois plus long que large et, lorsqu'on en fait le tour en bateau en restant toujours soigneusement à 700 m du rivage pour mieux la contempler, on parcourt 6398 m (le capitaine nous avait donné la distance en noeuds marins, mais nous avons converti!).
Au fait, pouvez-vous nous dire combien il y a d'arbres fruitiers sur cette île? On prendra 22/7 pour π.

11 - Le pistolet à calcul (coefficient 11)

Le diagramme ci-dessus comprend une ligne de 11 cases, et, au-dessous, une autre de 9 cases. Les cases de la première ligne étant remplies avec des nombres que l'on a choisis, on remplit celles de la seconde ligne à l'aide d'un pistolet à calcul pouvant glisser horizontalement. Pour chaque position du pistolet, on inscrit dans la case du bas du pistolet la somme des trois nombres apparaissant dans le haut du pistolet. Ainsi, dans l'exemple de la figure (à ne pas prendre en compte), 7 + 4 + 9 = 20.
Remplissez la ligne du haut avec des nombres entiers strictement positifs tous différents, de telle sorte que les nombres du bas soient 9 nombres entiers consécutifs rangés dans l'ordre croissant de gauche à droite, et dont le plus grand soit le plus petit possible.

Fin catégorie C2

12 - La pâte de coings (coefficient 12)

Fraîchement fabriquée maison, étalée sur un marbre, tous les gourmands de la famille en taillent un morceau. Au bout de 2 jours, il n'en reste qu'une livre (500 grammes), de forme ABCD. Gourmet et Gourmette désirent se la partager dans une dernière découpe prolongeant [AD]: OCD pour elle, OAB pour lui.

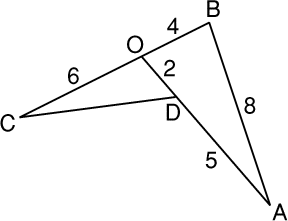
Au vu des dimensions (en largeur de doigts) de la figure, combien de grammes de pâte de fruit Gourmet aura-t-il?

13 - L'âge de Matteo (coefficient 13)

Matteo a quatre enfants: une fille aînée, et trois triplés. La fille aînée de Matteo, qui collectionne les poupées, en reçoit quatorze à chaque anniversaire, depuis son premier anniversaire. Quant aux triplés, la place venant à manquer chez Matteo, ils ont dû se contenter de 4 ours en peluche chacun à chaque anniversaire.
Matteo constate qu'en additionnant le carré de son âge avec les carrés des âges de ses enfants, puis en ajoutant 1, il obtient 1998. Par ailleurs, en ajoutant au carré de son âge le nombre de poupées et d'ours en peluche de ses enfants, puis en ajoutant à nouveau 1, il obtient le produit de l'âge de sa femme, qui a 29 ans, par l'âge de sa mère, qui a 71 ans.
Quel est l'âge de Matteo?

14 - Produit maximum (coefficient 14)

On a rangé les nombres impairs 1, 3, 5, 7, 9, 11, 13, et 15 dans un certain ordre x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, de telle manière que le produit:
(2-x₁) (4-x₂) (6-x₃) ... (16-x₈)
soit le plus grand possible.
Donnez dans l'ordre dans lequel on a rangé les nombres 1, 3, 5, 7, 9, 11, 13, 15.

Fin catégories L1 GP

15 - Les rectangles de grand-mère (coefficient 15)

Avec douze petits carreaux, on peut former trois rectangles différents.

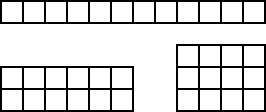
De la même façon, si on dispose d'un nombre de carreaux strictement inférieur à 200, quel nombre convient pour former six rectangles différents?

16 - La retraite des frères Rapetout (coefficient 16)

Les célèbres trois frères Rapetout, après une vie de rapines, ont acheté pour se retirer, trois terrains carrés jouxtant chacun par un côté un lac triangulaire où ils pourront s'adonner à leur loisir favori: la pêche à la ligne. Le triangle du lac, qui n'est pas isocèle, a une particularité: les tangentes de ses trois angles sont des nombres entiers. D'autre part, un côté de ce lac, qui n'est ni le plus grand, ni le plus petit, mesure 400 m.
Quelle est la somme des aires des terrains des trois frères Rapetout, exprimée en hm²? On arrondira, le cas échéant, à l'hm² le plus proche.

Fin catégories L2 HC