12^e Championnat International des Jeux Mathématiques et Logiques
finale internationale, 1^re séance, 28 août 1998

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Les allumettes (coefficient 1)

Pour faire un quadrillage de deux fois deux carreaux, on a utilisé 12 allumettes. Pour un quadrillage de trois fois trois carreaux, on a utilisé 24 allumettes.

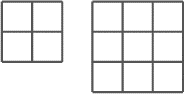
Combien faut-il d'allumettes pour composer un quadrillage de dix fois dix carreaux?

2 - Le père Veyre (coefficient 2)

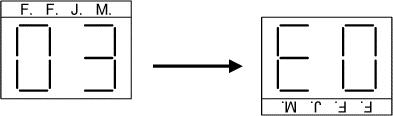
Un compteur à affichage digital indique les nombres de 01 à 99, dans l'ordre. Mais le père du petit Alan Veyre a tourné le compteur à l'envers (voir le dessin ci-dessus).
Alan regarde l'affichage défiler. Il voit alors 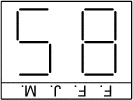affiché.
Que verra-t-il lors de l'affichage suivant?

Début catégorie C1

3 - Le quinze de la FFJM (coefficient 3)

Au rugby, il est possible de marquer trois points (drop ou pénalité), cinq points (essai non transformé) ou sept points (essai transformé). Lors d'une rencontre, l'équipe de la FFJM a marqué 20 points.

De combien de façons différentes peut-on compléter le tableau de scores ci-dessus?

4 - La gourmandise de K. Ramel (coefficient 4)

Karen Ramel va acheter des bonbons au magasin. Il y en a de plusieurs sortes, rangés dans des bocaux différents. Karen prend 2 bonbons dans le premier bocal, 4 bonbons dans le deuxième, 6 dans le troisième, et ainsi de suite en prenant 2 bonbons de plus dans chaque nouveau bocal. Après s'être servie dans le dernier bocal, elle revient en arrière et prend dans chacun des autres bocaux autant de bonbons qu'elle en avait pris lors du passage aller. K. Ramel a ainsi finalement 98 bonbons.
Combien y a-t-il de bocaux?

Début catégories C2 L1 L2 GP HC

5 - Les lampes (coefficient 5)

Sur ce tableau de bord, il y a deux lampes allumées.

À chaque fois qu'on touche à une lampe, celle-ci change d'état (si elle est allumée, elle s'éteint, et si elle est éteinte, elle s'allume) ainsi que ses deux voisines (ou son unique voisine si elle est au bord).
Combien faut-il toucher de lampes, au minimum, pour éteindre tout le tableau?

6 - Au coeur de la pyramide (coefficient 6)

La pyramide du pharaon Amathéfis III vient d'être achevée, mais horreur! On vient de s'apercevoir que les statues monumentales de la reine (marquées 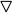sur le plan) et celles du pharaon (marquées ) ont été interverties.

Pour les remettre en place, il faut les déplacer très doucement. Il faut un jour pour en déplacer une d'une salle à une salle voisine, et on ne peut en déplacer qu'une par jour. D'autre part, elles sont si volumineuses qu'elles ne peuvent pas se croiser.
Combien de jours faudra-t-il pour les échanger?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Découpage préventif (coefficient 7)

Le père Francis a deux enfants et un terrain biscornu. Il veut en donner une partie à chacun de ses enfants, tout en en gardant une pour lui. Les trois parties doivent avoir la même forme (à un retournement près) et la même aire.

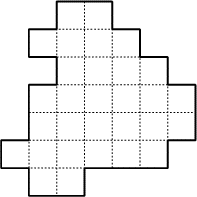
Quel est le découpage qui a été adopté (les lignes de découpe suivent le quadrillage)?

8 - Itinéraires à Rectangleville (coefficient 8)

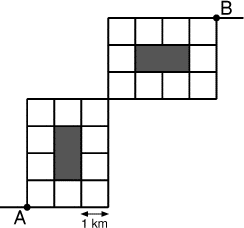
Mathias a invité Mathilde dans sa bonne ville de Rectangleville. Les rues correspondent aux côtés des petits carrés du plan dessiné ci-contre. Mathias habite en A, et ils décident d'aller en B pour visiter le musée des rectangles d'or.

Mathilde: Le chemin le plus court fait 14 km.
Mathias: Certes..., mais des chemins de cette longueur, il y en a beaucoup!
Mathilde: C'est vrai. C'est curieux, combien y en a-t-il?
Mathias: Heu..., c'est facile, il y en a...
Combien y a-t-il de chemins différents de 14 km, allant de A à B?

9 - Le Pythagore (coefficient 9)

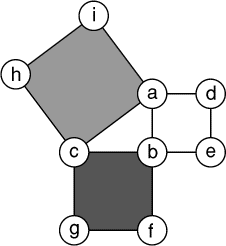
Remplacez les lettres a à i par les nombres de 1 à 9 de telle sorte que:

• la somme des nombres inscrits aux sommets du carré gris soit égale à la somme des nombres inscrits aux sommets du carré blanc augmentée de la somme des nombres inscrits aux sommets du carré noir;
• a < c, d < e < f < g et h < i.

Fin catégorie C1

10 - MGV (coefficient 10)

On vient de construire un nouveau métro à grande vitesse. Il est composé de deux voies circulaires séparées par un quai également circulaire, et il comporte 36 stations. Ces stations sont numérotées de 1 à 36 dans le sens des aiguilles d'une montre.
Les trains qui roulent sur la voie interne tournent dans le sens des aiguilles d'une montre et s'arrêtent toutes les 10 stations. Ceux qui roulent sur la voie extérieure roulent dans le sens contraire et s'arrêtent toutes les 13 stations. Le temps de parcours entre deux stations (qu'il y ait arrêt ou non) est de 1 minute.
En utilisant un changement, combien de temps mettra-t-on, au minimum, pour aller de la station n°1 à la station n°14?

11 - La tour prend garde (coefficient 11)

Cécile et Nicolas viennent chacun de construire une tour à l'aide de briques blanches et rouges. Les deux tours ont de nombreux points communs:

• elles ont la même hauteur;
• il n'y a jamais plus de trois briques rouges superposées;
• chaque brique blanche est surmontée d'au moins deux briques rouges.

Cependant, la tour de Cécile contient deux briques rouges de plus que celle de Nicolas.
Quelle est, en nombre de briques, la hauteur minimale de la tour de Cécile?

Fin catégorie C2

12 - Le gâteau de Valentin (coefficient 12)

Pour sa fête, Valentin a invité cinq amis. En cette occasion, sa mère a fait un gâteau ayant la forme ci-contre et l'a coupé en six. Bien sûr, les parts sont égales, de même surface et de même forme à un retournement près.

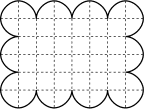
Faites le partage

13 - Le ver dans le cube (coefficient 13)

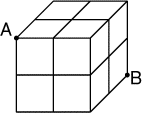
Un cube en bois très dur de 1 dm de côté a été construit en assemblant huit cubes de 0,5 dm de côté avec de la colle. Un ver souhaite aller du sommet A au sommet B du grand cube. Il peut: soit ramper sur la surface du grand cube, soit creuser dans la colle pour se faufiler entre les petits cubes, mais il est incapable de creuser dans le bois qui constitue les petits cubes.
Quelle distance, au minimum, doit-il parcourir?
Si besoin est, on prendra 1,414 pour √2; 1,732 pour √3; 2,236 pour √5. On arrondira la réponse au millimètre.

14 - Multiplication magique (coefficient 14)

Dans un carré 3 × 3, on a placé des entiers positifs, tous distincts, de telle sorte que les produits des trois nombres écrits dans une même ligne ou une même colonne soient tous égaux. En outre, le plus grand entier qui apparaît dans le carré est le plus petit possible.

Que vaut le produit des trois nombres d'une même ligne?

Fin catégories L1 GP

15 - L'héritage de Francis (coefficient 15)

Le vieil oncle d'Amérique, né en 1898, vient de mourir. Lorsque le notaire lui lit la partie qui le concerne, Francis s'entend dire: ... à Francis qui aime bien les nombres, je lègue la plus petite somme en dollars telle que, si on la divise par 98, il reste 20 dollars; si on la divise par 598, il reste 120 dollars; si on la divise par 1998, il reste 400 dollars; et enfin, si on la divise par 2898, il reste 580 dollars... et si Francis est capable de trouver le montant exact de cette somme en moins d'une demi-heure, elle est à lui, sinon cette somme sera à répartir entre mes autres héritiers!.
Soyez aussi efficace que Francis, trouvez le nombre exact de dollars!

16 - Sauts de puce (coefficient 16)

Une puce visite les cases d'un échiquier de 6 cases sur 6 cases (les cases mesurent 1 cm de côté). Elle saute alternativement horizontalement et verticalement, et parcourt toutes les cases de l'échiquier avant de revenir à son point de départ. Elle ne retombe jamais sur une case où elle s'est déjà posée, sauf à la fin.
Les sauts sont rectilignes et mesurent 1, 2, 3, 4 ou 5 cm (on suppose que la puce saute toujours du centre d'une case au centre d'une autre case). Sur l'exemple ci-contre où l'on a légèrement déplacé certains points de chute de la puce afin de rendre le parcours plus visible, la longueur totale du parcours est égale à 60 cm.

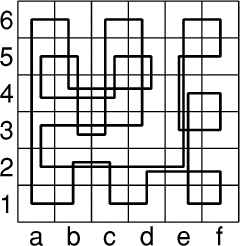
Donnez la longueur du parcours le plus court possible et celle du parcours le plus long possible.

Fin catégories L2 HC