12^e Championnat International des Jeux Mathématiques et Logiques
finale internationale, 2^e séance, 29 août 1998

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Alignement fou (coefficient 1)

On juxtapose tous les nombres à partir de 1:
1 2 3 4 5 6 7 8 9 10 11 12 13 ......
Quel est le 98^ème chiffre écrit?

2 - Le concours (coefficient 2)

Dans un concours de beauté, le règlement stipule: La dotation totale des prix est de 4000 F. Le premier prix recevra 400 F, le deuxième 300 F, et la somme restante sera partagée à égalité parmi tous les autres participants.
Le troisième a obtenu un prix plus important que le deuxième. Combien y avait-il de participants, au maximum?

Début catégorie C1

3 - Le bon élève (coefficient 3)

Julien vient de terminer une multiplication. Il a effectué le produit de 64 par 48, et il a trouvé 3112. Le maître s'approche: C'est très bien, Julien, tu es en progrès, tu as fait une seule faute, et c'est en multipliant 6 par 8.
Que vaut 6 × 8 pour Julien?

4 - Cadet Roussel a 3 garçons (coefficient 4)

Les âges des trois garçons sont des nombres entiers. Le produit de leurs âges est de 18. Dans un an, le produit de leurs âges sera égal à 60.
Quels sont les âges de ses trois fils?

Début catégories C2 L1 L2 GP HC

5 - Un travail de titan (coefficient 5)

Au fond de l'océan, un plongeur découvre l'épave d'un navire. Malheureusement, le nom du bateau est illisible. Il comporte 7 lettres, mais le plongeur ne distingue que les 3 dernières: N I C. Les lettres apparaissant dans le nom du bateau sont A, I, C, N et T. Les consonnes alternent avec les voyelles. L'une des voyelles est répétée deux fois, de même que l'une des consonnes. De retour à la surface, le plongeur énumère tous les noms possibles. Combien y en a-t-il?

6 - La tablette de Nicolas (coefficient 6)

Nicolas veut partager la tablette de chocolat (entamée) représentée ci-contre entre ses quatre neveux. Bien sûr, les parts doivent être égales et de même forme (éventuellement après retournement). De plus, Nicolas s'interdit de couper un carré.

Réalisez le partage.

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - L'effet miroir (coefficient 7)

Anna est en train de se faire belle, car elle sort aujourd'hui... Soudain, elle aperçoit sa pendule dans le miroir (c'est une pendule à aiguille et elle est à l'heure). Horreur, il est exactement l'heure où elle devrait partir et elle n'est pas prête! Elle jette alors un coup d'oeil à l'horloge de l'église (qui est à l'heure), par la fenêtre, et elle constate qu'elle dispose encore d'exactement une heure pour se préparer.
Dessinez les positions de la petite et de la grande aiguille de l'horloge de l'église.

8 - C'est pas sorcier (coefficient 8)

Lors d'une cérémonie, le grand sorcier présente une corbeille à chacun des 97 participants (chacun d'eux, comme le grand sorcier, est venu avec son collier orné de dents de jaguar et de plumes de vautour). Chacun d'eux peut alors, à son tour:

• soit prendre une dent de jaguar et une plume de vautour,
• soit prendre deux plumes de vautour, mais il doit alors déposer une dent de jaguar dans la corbeille.

La cérémonie s'arrête lorsque le contenu de la corbeille ne peut plus être modifié. Au départ, il y avait 8 dents de jaguar et 9 plumes de vautour dans la corbeille.
Combien y a-t-il de dents de jaguar et de plumes de vautour dans la corbeille à la fin de la cérémonie?

9 - Le tapis triangulaire (coefficient 9)

Un riche commerçant du pays de Tribord avait fait tisser un tapis dont il n'était pas peu fier. Aussi se vanta-t-il auprès d'une autorité locale: Mon tapis a la forme d'un triangle équilatéral. Il est constitué par un pavage triangulaire (voir dessin). Le bord est constitué de triangles noirs; l'intérieur est formé de petits triangles blancs, et, chose curieuse, il y a autant de petits triangles sur le bord qu'à l'intérieur....

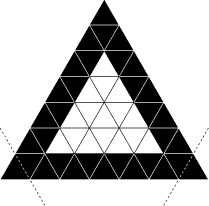
Voyons cela, dit le notable, qui se piquait d'un peu d'arithmétique!
José, le fils du commerçant, comprit que son père s'était engagé un peu vite, et, craignant le courroux du haut personnage, il profita d'un moment d'inattention de son père pour supprimer rapidement un petit triangle dans deux coins du tapis, de façon à rétablir l'égalité annoncée.
De combien de petits triangles le tapis était-il constitué avant l'intervention de José?

Fin catégorie C1

10 - Les deux cylindres (coefficient 10)

Le professeur de Mathias et de Mathilde a donné à chacun d'eux une feuille de carton rectangulaire de mêmes dimensions, avec la consigne suivante: Roulez la feuille en cylindre et calculez le volume du cylindre obtenu.
Mathias et Mathilde ont chacun obtenu un résultat qu'ils comparent. Stupeur, leurs cylindres sont différents!... En y regardant de plus près, le volume obtenu par Mathias est huit fois plus grand que celui trouvé par Mathilde.
Le périmètre de la feuille de carton est de 72 cm. Quelle est la longueur du plus grand côté?
Pour d'éventuels calculs, on prendra 355 / 113 pour π.

11 - Fiers Fanions et Jolis Mouchoirs (coefficient 11)

Au supermarché FFJM (Fiers Fanions et Jolis Mouchoirs), tous les prix sont des nombres entiers de francs, et un fanion coûte plus cher qu'un mouchoir. Alice a pris un fanion et un mouchoir. Elle remarque que pour écrire les deux prix, il faut utiliser quatre chiffres distincts. Mauvaise surprise: la caissière annonce une somme à payer supérieure de 359 F au prix total, qu'Alice avait calculé mentalement (sans se tromper!).
Après vérification, on constate que la caissière, étourdie, a multiplié les deux prix au lieu de les ajouter.
Quel est le prix d'un fanion?

Fin catégorie C2

12 - Petites boîtes (coefficient 12)

n°	d1	d2	d3
1	11	20	22
2	9	24	18
3	26	28	21
4	18	23	25
5	24	10	10
6	12	8	15
7	14	14	17
8	16	13	7

On dispose de huit boîtes de carton de forme parallélépipédique dont les trois dimensions sont indiquées dans le tableau ci-contre. On prend une des boîtes, on la pose sur le sol et on découpe la face du dessus que l'on supprime. On choisit une deuxième boîte que l'on pose, sans forcer, à l'intérieur de la première boîte. On découpe alors la face du dessus de cette deuxième boîte, qui peut dépasser de la première. On essaie ensuite de poser une troisième boîte, toujours sans forcer, à l'intérieur de la seconde. En continuant de la sorte, on emboîte ainsi le plus grand nombre possible de cartons pris parmi les huit. À chaque étape, on découpe la face du dessus, qui peut dépasser ou non de la boîte précédente.
Écrivez les numéros des boîtes utilisées, de la première à la dernière posée.

13 - Q.C.M. autoréférent (coefficient 13)

Pour chacune des cinq questions suivantes, choisir une réponse (A, B, C ou D) de telle sorte que les cinq affirmations soient toutes vraies simultanément.
1) La première question dont la réponse est C porte le numéro

    (A) 2         (B) 3         (C) 4         (D) 5

2) Les deux seules questions consécutives qui ont la même réponse sont

    (A) 1 et 2    (B) 2 et 3    (C) 3 et 4    (D) 4 et 5

3) Le nombre de questions dont la réponse est A est

    (A) 0         (B) 1         (C) 2         (D) 3

4) Cette question a la même réponse que la question

    (A) 5         (B) 1         (C) 2         (D) 3

5) Cette question a pour réponse

    (A) A         (B) B         (C) C         (D) D

14 - La citerne (coefficient 14)

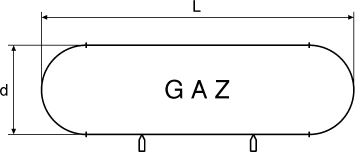
Le père Missif vient de faire installer une superbe citerne à gaz pour sa maison. Les deux dimensions (longueur hors tout et diamètre) de la citerne sont des nombres entiers de décimètres.
Fin calculateur, le père Missif calcule aussitôt l'aire et le volume de sa citerne. Il obtient 6,48 π m² pour l'aire, et 1,8 π m³ pour le volume. Quel est le diamètre de la citerne du père Missif? On donnera la réponse en dm.

Fin catégories L1 GP

15 - Le coup de chiffon (coefficient 15)

Thomas Tématik est content de lui: il vient de trouver une position remarquable de seize nombres disposés en quatre hexagones. Les nombres, tous différents, sont compris entre 7 et 24, et la somme des nombres disposés aux sommets de chaque hexagone est égale à 100. Fier de lui, Thomas laisse sur son bureau les jetons dont il s'est servi, et il sort faire un tour...

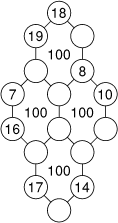
Sa femme de ménage en profite pour nettoyer un peu! Mais un malheureux coup de chiffon fait rouler huit jetons sur le sol. Consciente d'avoir fait une bêtise, elle ramasse les jetons, constate qu'il n'y a ni 9, ni 15, et essaie de les remettre en place.
Aidez-la!

16 - Le terrain du père C. Cuté (coefficient 16)

Le père Cuté, Charles de son prénom, qui s'imagine que tout le monde lui en veut, possède un terrain de forme triangulaire. Les longueurs des côtés de ce terrain sont toutes des nombres entiers de mètres, de même que les rayons respectifs de ses cercles inscrit et circonscrit.
Charles, qui se méfie de tout le monde, nous a seulement confié que le rayon du cercle circonscrit à son terrain est égal à 169 mètres, que la distance entre les centres des cercles inscrit et circonscrit vaut 39 mètres, et que son terrain a une aire de 34 560 m².
Quel est le périmètre du terrain de Char. Cuté?

Fin catégories L2 HC