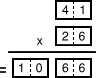12e Championnat International des Jeux Mathématiques et Logiques
finale régionale, 16 mai 1998
Catégories
- Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
- Catégorie C1 (6e, 5e): problèmes 3 à 9, 2 h.
- Catégorie C2 (4e, 3e): problèmes 5 à 11, 3 h.
- Catégorie L1 (2e, 1e, terminale): problèmes 5 à 14, 3 h.
- Catégorie GP (grand public): problèmes 5 à 14, 3 h.
- Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
- Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.
(Calculatrices interdites)
Énoncés des problèmes
Début catégorie CM
- 1 - Problème vosgien
(coefficient 1)
- Placer les 4 chiffres du nombre 1998 dans les cases afin que
le résultat soit le plus grand possible:

- 2 - Les dominos de la FFJM
(coefficient 2)
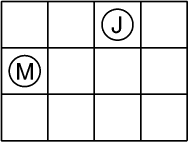
- Les six dominos de la FFJM sont représentés
ci-contre.

Placez-les dans la grille 3 × 4, sans les tourner, afin
que dans chaque ligne figurent 2 fois le F, 1 fois le J et 1 fois le M.
Début catégorie C1
- 3 - La FFJM en cube
(coefficient 3)
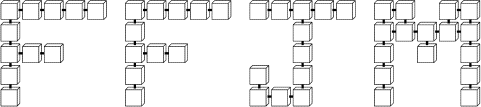
Pour écrire FFJM avec des cubes, Gilles a eu besoin de
50 cubes. Il les a assemblés conformément au schéma ci-dessus en collant
les faces adjacentes. Chacun des 48 tirets épais indique un point de colle.
Gilles décide alors de peindre toutes les faces non collées des cubes.
Combien de faces de petits cubes devra-t-il peindre?- 4 - La bande de papier
(coefficient 4)

On plie une bande de papier de largeur
1 cm en trois endroits, puis on
colle les deux extrémités de la bande qui se superposent en un petit
carré de 1 cm sur
1 cm. Cette bande entoure un carré
d'aire 100 cm². Quelle
était la longueur de la bande de papier avant pliage?
Début catégories C2 L1 L2 GP HC
- 5 - L'arbre de la FFJM
(coefficient 5)
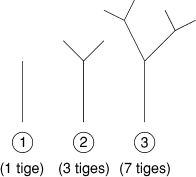
Avant le départ du premier Championnat, Michel avait planté une graine.
Après la fin du premier Championnat, cette graine avait donné une tige.
À la fin du second Championnat, chaque extrémité avait donné naissance
à deux nouvelles tiges; notre arbre en comportait 3. Nous sommes au
douzième Championnat. À son terme, combien de tiges l'arbre de la
FFJM comportera-t-il?- 6 - Le trésor du pharaon
(coefficient 6)
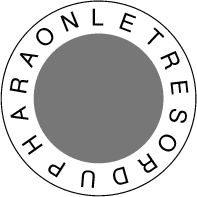
Mathilde et Mathias sont à la recherche du trésor du pharaon. Se trouvant
derrière une porte, ils remarquent une inscription circulaire: Le trésor
du Pharaon
. Un vieux sage apparaît alors et leur dit:
Je sais que vos intentions sont pures. Aussi vais-je vous révéler
comment passer cette porte. Il suffit d'appuyer sur la bonne lettre.
Mais comment savoir quelle lettre est bonne?
, s'enhardit Mathilde.
Il faut partir de la première lettre A du mot PHARAON en suivant les
instructions suivantes: si on est sur une consonne, on avance de 3 lettres
dans le sens des aiguilles d'une montre; si on aboutit sur une voyelle, on
doit reculer de deux lettres... et si on est sur le P de PHARAON, on avance
de cinq lettres. En considérant le premier A de PHARAON comme la première
lettre, la 1998ème lettre est la bonne!
Et le sage s'éclipsa.
Sur quelle lettre doivent-ils appuyer pour que la porte
s'ouvre?
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - Multiplication de dominos
(coefficient 7)
- En
multipliant
le domino 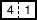 par le domino
par le domino 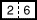 , on obtient 1066, score
que l'on peut écrire avec les dominos
, on obtient 1066, score
que l'on peut écrire avec les dominos 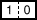 et
et 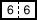 .
.
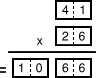
Quels dominos permettent d'obtenir le score le plus élevé? note:
On rappelle qu'un jeu de dominos comprend 28 dominos différents, de 0-0
à 6-6. On dispose d'un seul jeu de dominos et ceux-ci portent des points
(ou une absence de point pour 0) et non des chiffres.
- 8 - Partage de triangles
(coefficient 8)
- J'ai devant moi trois triangles rectangles non isocèles identiques.
Si je coupe l'un d'eux selon la hauteur (xy) issue du sommet de l'angle
droit, j'obtiens quatre triangles dont deux sont encore identiques. Je
peux à nouveau couper l'un des quatre triangles rectangles selon la
hauteur issue du sommet de l'angle droit, et répéter cette opération
autant de fois que je le souhaite sur n'importe quel triangle rectangle
de la figure à un instant donné.
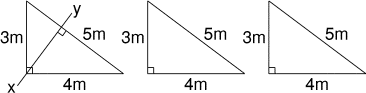
À partir des trois triangles de départ, combien de coupes
seront nécessaires, au minimum, pour obtenir des triangles tous
différents?
- 9 - Nombre à deux chiffres
(coefficient 9)
- On choisit un nombre à deux chiffres, puis on multiplie ce nombre
par le produit de ses chiffres. On obtient 336.
Quel était le nombre choisi au départ?
Fin catégorie C1
- 10 - Somme de puissances
(coefficient 10)
- Dans la somme de puissances
ab + cd + ef, on
remplace les lettres a, b, c, d, e et f par les nombres 1, 2, 3, 4, 5 et 6,
mais pas forcément dans cet ordre. On peut ainsi avoir, par exemple,
16 + 52 + 43 = 90.
Mais quel est le plus grand résultat que l'on puisse obtenir?
- 11 - Sur toutes les pages lues
(coefficient 11)
- Le jeune Paul reprend avidement la lecture de son roman, un livre
de moins de 200 pages.
Avant de se replonger dans un nouveau chapitre, qui débute au début d'une
page de gauche, il a le temps de remarquer que la somme de tous les chiffres
servant à numéroter les deux pages du livre ouvert est égale à 31.
Plus tard, la fatigue le gagnant, il décide de s'arrêter à la fin d'une
page de droite, qui est aussi la fin d'un chapitre, ... non sans avoir
remarqué que la somme des chiffres servant à numéroter les deux pages
est égale à 19.
Toutes les pages de gauche sont numérotées à l'aide d'un nombre pair.
Combien de pages Paul a-t-il lues?
Fin catégorie C2
- 12 - Courses de rentrée
(coefficient 12)
- Jeannot fait ses courses pour la rentrée et achète un grand cahier,
un taille-crayon, un compas, un rapporteur et un classeur. Il ne se
souvient plus du prix de chaque objet, ni du prix payé pour l'ensemble,
mais, fin calculateur, il a remarqué qu'en multipliant le prix du cahier
(exprimé en francs) par celui du taille-crayon, il trouvait un résultat
égal à 36. De même, le produit du prix du taille-crayon par celui du
compas donne 54, le produit du prix du compas par celui du rapporteur 72,
le produit du prix du rapporteur par celui du classeur, 108, et le produit
du prix du classeur par celui du cahier 144.
Quel est le prix du taille-crayon?
- 13 - Le champ trapézoïdal
(coefficient 13)
- Le père Itoine possède un champ en forme de trapèze. Ses quatre côtés
mesurent des nombres entiers de mètres, et son aire s'exprime par un nombre
entier de mètres carrés.
Par ailleurs, on sait que la grande base mesure
70 m, et que les deux côtés autres que
les bases mesurent respectivement 104 et 50 mètres.
Combien mesure la petite base du champ du père Itoine?
- 14 - Les 13 nombres
(coefficient 14)
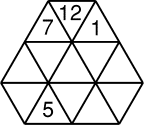
Complétez le dessin ci-contre avec les nombres de 1 à 13 (4 nombres
sont déjà placés) de telle sorte que:
- deux cases voisines par un côté ne contiennent jamais deux nombres
consécutifs;
- deux cases voisines par un côté ne contiennent jamais deux nombres
ayant un diviseur commun autre que 1.
Fin catégories L1 GP
- 15 - Le tour de José
(coefficient 15)
- M. Gefonse, José pour les intimes,
adore faire des tours numériques à ses amis. Dernièrement, j'ai assisté à
l'un d'eux.
Il fait choisir à quelqu'un un nombre compris entre 1 et 2000, nombre que
cette personne garde évidemment secret. José demande simplement de faire
les divisions de ce même nombre par 3, par 23 et par 29 et de lui donner
les restes des divisions dans cet ordre. Ainsi, Gilles, qui avait choisi
1998, annonce les trois restes 0, 20 et 26.
Le truc de José est de multiplier chacun de ces restes par un nombre
magique (un pour chaque reste), d'additionner le tout et de faire une
division par un autre nombre magique, le reste de cette division lui
donnant le nombre choisi au départ!
Après que j'ai beaucoup insisté, José finit par lâcher une formule:
Si les restes respectifs des divisions par 3, 23 et 29 sont
r1, r2 et
r3, je calcule
ar1 + br2 + cr3
et je divise le résultat par d. Le reste me donne le
nombre n choisi. Aucun des quatre nombres a,
b, c, d ne dépasse 3000. Ne le
dévoilez à personne!
Quels sont, dans cet ordre, les nombres a, b,
c et d?
Note: une seule solution demandée.
- 16 - Raréfaction des pions
(coefficient 16)
- Sur les cases d'un plan quadrillé illimité, on pose 61 pions au
hasard (un par case). Après cette pose, on retire le plus petit nombre
de pions possible N tel que deux cases prises parmi les
61 - N cases ayant conservé un pion n'aient jamais
ni un côté commun, ni un sommet commun.
Quelle est la plus grande valeur possible de N?
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org










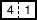 par le domino
par le domino 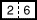 , on obtient 1066, score
que l'on peut écrire avec les dominos
, on obtient 1066, score
que l'on peut écrire avec les dominos 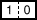 et
et 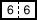 .
.