12^e Championnat International des Jeux Mathématiques et Logiques
1/4 de finale individuels

Date limite: 31 décembre 1997. Vous pouvez trouver les énoncés des problèmes, un bulletin-réponse et toutes les autres infos sur le championnat dans le numéro 60 du magazine Tangente.

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14.
• Catégorie GP (grand public): problèmes 5 à 14.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16.
• Catégorie HC (haute compétition): problèmes 5 à 16.

Énoncés des problèmes

Début catégorie CM

1 - Des vacances ensoleillées (coefficient 1)

Aimé et Théo sont deux amis qui ont passé leurs dernières vacances ensemble. À la fin de chaque demi-journée, Aimé a noté sur son carnet de bord un S si elle avait été plutôt ensoleillée, et un N comme nuages dans tous les autres cas.
À la fin de leur séjour, nos deux amis font le point:
Aimé: T'as vu, nous avons eu 30 demi-journées de soleil et 16 demi-journées de nuages.
Théo: Exact! Et regarde, il y a exactement 10 journées qui ont été ensoleillées du matin au soir.
Combien de journées entièrement nuageuses ont-ils eu pendant leur séjour?

2 - Les deux patrons (coefficient 2)

Voici deux patrons identiques de solides.

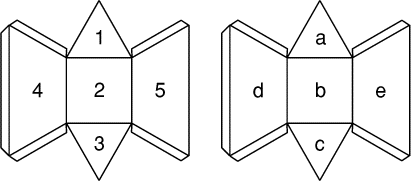
On assemble ces deux solides.
Quelles faces faut-il mettre en vis-à-vis pour construire une pyramide à base triangulaire (ou tétraèdre)?

Début catégorie C1

3 - La FFJM dans tous ses états (coefficient 3)

Avec les lettres F, F, J et M, il est possible de former différents sigles: FFJM (Fédération Française des Jeux Mathématiques), MFJF (Mouvement Furtif des Jeunes Frondeurs), ....
Combien de sigles peut-on ainsi écrire, en comptant les deux exemples donnés?

4 - Pentaminos troués (coefficient 4)

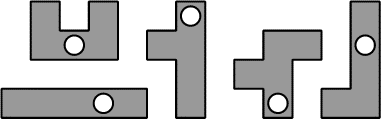
Nina possède cinq pentaminos troués (les trous sont circulaires). Elle désire les placer de telle sorte que:

• l'assemblage forme un carré
• il ne doit y avoir qu'un seul trou par colonne et par ligne
• les pièces peuvent être retournées

Aidez Nina en complétant la figure ci-contre.

Début catégories C2 L1 GP L2 HC

5 - Quand on aura 20 ans... (coefficient 5)

1998 est divisible par la somme de ses chiffres: 1998 / (1+9+9+8) = 74. De plus, les chiffres composant le nombre obtenu sont tous différents de ceux du millésime de l'année.
Quelle sera la prochaine année à vérifier la même propriété?

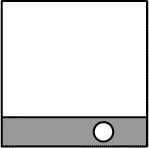
6 - Le concours de coloriage (coefficient 6)

La ville d'Hexacarré a décidé d'adopter un fanion qui sera porté sur tous les véhicules officiels. Ce fanion devra être composé de six carrés disposés en rectangle (voir dessin), et comporter trois couleurs: 1 carré bleu, 2 carrés blancs et 3 carrés rouges. Un concours est ouvert... à qui trouvera la disposition la plus belle.
Quel est le nombre maximum de propositions différentes que les organisateurs du concours pourront recevoir?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - L'aïeul (coefficient 7)

Maurice, l'arrière grand-père de José, n'est certes pas centenaire, mais il a tout de même un âge très avancé. Tout ce que l'on peut vous dire c'est que l'année dernière, son âge était un multiple de huit, et que l'année prochaine, il sera un multiple de sept.
Quel est l'âge de Maurice?

8 - Le partage (coefficient 8)

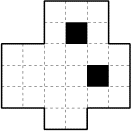
Sur un terrain se trouvent deux étangs. Ce terrain, sans les étangs, doit être partagé en quatre parties superposables. Chaque parcelle, formée de petits carrés entiers, doit être d'un seul tenant.
Faites le partage.

9 - Aire maximale (coefficient 9)

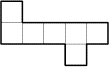
Bernard et Gilles ont fabriqué six pièces retournables identiques à celle-ci (voir dessin). Ils vont réaliser une chaîne fermée avec les six pièces de telle sorte que l'aire de la figure intérieure soit la plus grande possible. Deux pièces doivent toujours se toucher par au moins un côté d'un petit carré.
Quelle est l'aire maximale?

Fin catégorie C1

10 - Curvica triangulaire (coefficient 10)

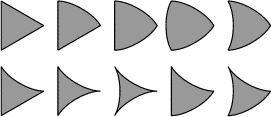
À son ami Jean qui a créé le jeu curvica, Francis a envoyé le problème suivant:
Dix pièces composées à partir de triangles équilatéraux sont données (figure ci-dessus). On peut les tourner et les retourner à loisir. Il s'agit ici de composer la figure ci-contre...

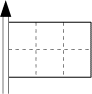
Trouverez-vous avant Jean?

11 - La pyramide de nombres (coefficient 11)

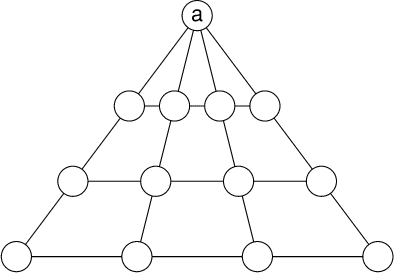
On place les nombres de 1 à 13 dans les cercles de cette pyramide de nombres, de telle sorte que la somme de 4 nombres formant un alignement (dans n'importe quelle direction) soit toujours la même.
Quel nombre doit-on placer en a?
Répondez 0 si vous pensez qu'une telle pyramide est impossible à réaliser.

Fin catégorie C2

12 - Mots croisés (coefficient 12)

Maurice Croisé (dit Momo), Victor Hizontal et Sylvère Tical sont trois fanas de mots croisés. Aujourd'hui, il sont en face d'une grille vierge un peu bizarre et difficilement exploitable. Il faut dire que la méthode utilisée pour la créer est pour le moins originale.
Cette grille comporte 19 lignes et 98 colonnes.
Victor a écrit l'alphabet dans l'ordre, ligne par ligne, à raison d'une lettre par case, en commençant par la lettre A dans la case (1;1) et en répétant l'alphabet autant de fois que nécessaire pour aller jusqu'à la case (19;98).
Son collègue Sylvère en a fait autant, mais en travaillant quant à lui colonne par colonne.
Maurice a alors noirci toutes les cases où apparaissait deux fois la même lettre, comme par exemple les deux A de la case (1;1).
Combien la grille comporte-t-elle de cases noires?

13 - Un angle très occupé (coefficient 13)

Le point O est le centre commun des cercles C₁ et C₂ de rayons respectifs R₁ = 10 cm et R₂ = 5 cm. Le point P est situé sur le cercle C₂. Le point Q a été choisi sur le cercle C₁ de telle manière que l'angle OQP soit le plus grand possible.
Donnez la mesure en degrés de l'angle OQP.

14 - L'étrange surface (coefficient 14)

ABC est un triangle équilatéral de côté 10 cm. On projette le côté [AB] de ce triangle orthogonalement sur toutes les droites passant par C.
Quelle est l'aire de la surface formée par toutes les projections?
On donnera cette aire en cm², arrondie au cm² le plus proche (on prendra 1,732 pour racine de 3 et 3,1416 pour π).

Fin catégories L1 GP

15 - Triangle presque équiangle (coefficient 15)

Un triangle ABC est tel que AB = 10 cm et AC = 26 cm.
Quelle longueur faut-il donner au côté BC pour que le plus petit angle du triangle ABC soit le plus grand possible?
On donnera la réponse en millimètres, si besoin est arrondie au millimètre le plus proche.

16 - Passera, passera pas? (coefficient 16)

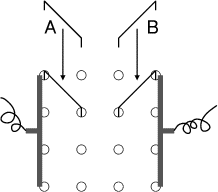
On dispose de deux électrodes métalliques entre lesquelles se trouve un réseau à mailles carrées de 3 petits carrés sur 3. Pour chaque petit carré élémentaire de ce réseau, on peut enficher une barrette conductrice sur une des diagonales (les deux positions possibles sont illustrées en A et B).

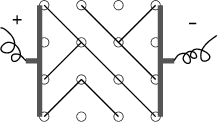
Gilles enfiche 9 barrettes (une par petit carré), en choisissant à chaque fois au hasard une des deux diagonales (un exemple est donné ci-contre). Il applique ensuite une tension électrique aux bornes des deux électrodes.
Quelle est la probabilité pour que le courant passe? On donnera la réponse sous la forme d'une fraction irréductible.

Fin catégories L2 HC