14^e Championnat International des Jeux Mathématiques et Logiques
demi-finale, 18 mars 2000

Catégories

• Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
• Catégorie C1 (6^e, 5^e): problèmes 3 à 9, 2 h.
• Catégorie C2 (4^e, 3^e): problèmes 5 à 11, 3 h.
• Catégorie L1 (2^e, 1^e, terminale): problèmes 5 à 14, 3 h.
• Catégorie GP (grand public): problèmes 5 à 14, 3 h.
• Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
• Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.

(Calculatrices interdites)

Énoncés des problèmes

Début catégorie CM

1 - Histoire de famille (coefficient 1)

Dans une famille, chacun des enfants peut déclarer avoir au moins un frère et une soeur.
Combien d'enfants, au minimum, cette famille comporte-t-elle?

2 - Il est fou, ce Romain! (coefficient 2)

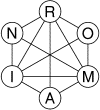
Romain a écrit son nom avec six jetons portant chacun une lettre. Il propose à Marion de procéder à des échanges de deux lettres reliées par un segment de façon à transformer ROMAIN en MARION.
Quel est le nombre minimum d'échanges nécessaires à cette transformation?

Début catégorie C1

3 - La poste et vous (coefficient 3)

Michel n'a pas voulu me donner le code postal de sa ville. Il m'a seulement répondu:

• comme tout code postal français, il comporte cinq chiffres
• la somme du premier chiffre et du deuxième est 17
• la somme du deuxième chiffre et du troisième est 15, de même que la somme du troisième et du quatrième
• la somme des deux derniers est 9
• enfin, la somme du dernier et du premier est 8.

Quel est le code postal de la ville de Michel?

4 - Des pommes, des poires... (coefficient 4)

Michèle et Patrick reçoivent aujourd'hui sept personnes à dîner. Pour le dessert, ils envisagent d'aller cueillir des pommes et des poires au verger.
Mais le chemin est long et ils savent qu'à eux deux, ils ne peuvent porter plus de 7 kg de fruits. De plus, ils veulent que chacun de leurs invités ait le choix. Une pomme pèse 300 g tandis qu'une poire ne pèse que 200 g. Quel est le nombre maximum de fruits qu'ils peuvent ramener?

Début catégories C2 L1 L2 GP HC

5 - Bon anniversaire (coefficient 5)

Pour les douze ans de Mathilde, ses parents ont commandé au pâtissier des petits fours très particuliers... en forme de triangles, et de périmètre 12 cm. De plus, les côtés des triangles mesurent tous des nombres entiers de centimètres.
Combien de formes différentes le pâtissier va-t-il pouvoir réaliser (on peut les retourner)?

6 - Le numérotage des pages (coefficient 6)

Pour numéroter toutes les pages d'un gros cahier, à partir de la page n°1, Audrey a utilisé deux fois plus de chiffres que le nombre de pages de ce cahier.
Combien ce cahier comporte-t-il de pages?

Fin catégorie CM

Attention! Pour les problèmes 7 à 16, pour chaque problème susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on demande le nombre de solutions, et on prévoit l'emplacement pour écrire deux solutions. Ceci ne signifie pas que ces problèmes ont toujours plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!

7 - Les garde-manger de Mirô (coefficient 7)

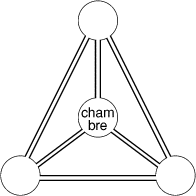
Le terrier de Mirô, la taupe, comprend quatre pièces reliées par six galeries. L'une de ces pièces est la chambre à coucher de Mirô, et les trois autres lui servent de garde-manger: Mirô y entrepose ses réserves de vers de terre.
La mémoire de Mirô étant aussi bonne que sa vue, pour s'y retrouver, celle-ci a placé dans chaque galerie un petit écriteau sur lequel elle a inscrit la différence entre les nombres de vers de terre (le plus grand moins le plus petit) des deux pièces situées aux extrémités de cette galerie. Voici ce qu'indiquent les six écriteaux aujourd'hui: . Quels sont les nombres de vers de terre contenus dans les trois garde-manger de Mirô, du moins rempli au mieux rempli? Note: la chambre à coucher ne contient, bien sûr, aucun ver de terre.

8 - Les barres chocolatées (coefficient 8)

Mes quatre cousins arrivent dimanche matin pour le petit déjeuner à la maison, pour douze jours de vacances. Ils sont aussi gourmands que nous! Heureusement, ma mère, prévoyante, a acheté 168 barres chocolatées afin que chacun puisse, pendant les douze jours, en recevoir une à chaque petit déjeuner et à chaque goûter. Hélas, au soir du neuvième jour, nos cousins doivent interrompre leur séjour et rentrer chez eux. Nous continuons, malgré leur absence, à déguster les barres chocolatées à la même fréquence.
Quel jour de la semaine croquerons-nous la dernière barre?

9 - 12 × 5 = 6 × 10 (coefficient 9)

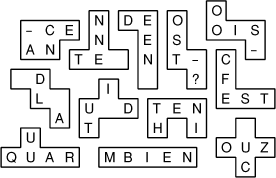
Fin catégorie C1

10 - Embrouille sur la feuille de match (coefficient 10)

Pendant les derniers matches avant la finale de la coupe de basket, nous avons bien vu dans les tribunes un espion de notre future équipe adverse. Il notait notre tactique habituelle. Il nous faut perturber les repères qu'il a pu prendre. Nous avons donc décidé de redistribuer nos cinq maillots numérotés de façon qu'aucun de nous cinq ne porte son numéro habituel.
De combien de manières pouvons-nous effectuer cette redistribution?

11 - L'alphabet du millénaire (coefficient 11)

A = 2000
B = A - 999
C = A + B - 998
D = A + B + C - 997
.
.
.
.
.
Z = A + B + C + .......... + Y - 975
Combien vaut Z?

Fin catégorie C2

12 - La calculatrice de Jean-Christophe (coefficient 12)

Sur la calculatrice de Jean-Christophe, il ne reste que trois des touches de 1 à 9 qui fonctionnent. En utilisant uniquement ces trois touches, Jean-Christophe ajoute les six nombres possibles à deux chiffres distincts qu'il peut former.
Ô miracle, la somme qui s'affiche utilise encore ces trois mêmes chiffres.
Que vaut cette somme?

13 - Les deux cônes (coefficient 13)

Mathilde et Mathias sont au collège. Leur professeur a donné à chaque groupe de deux élèves un disque de papier de 20 cm de diamètre. La consigne est de découper le disque en deux secteurs et d'en faire deux cônes en rapprochant les bords coupés.

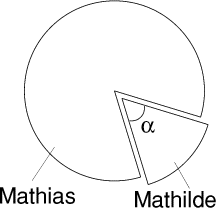
Chacun s'affaire en coupant suivant son bon plaisir. Ainsi Mathilde a découpé un secteur et elle donne la partie restante à Mathias (voir figure).
Soigneusement, du papier adhésif est collé pour achever la mise en forme des deux cônes. Ils peuvent alors constater que le cône de Mathilde est deux fois plus haut que celui de Mathias!
Quelle est la valeur de l'angle α du secteur découpé par Mathilde, arrondi au degré le plus proche?
Pour d'éventuels calculs, on prendra 2,236 pour √5; 2,646 pour √7; 3,317 pour √11; 3,606 pour √13 et 3,1416 pour π.

14 - Une multiplication (coefficient 14)

            * * * *
       ×    * * 7 *
       -------------
          * * * * *
          * * * *
      * * * *
  ------------------
  = * * * * * * * *

Dans cette multiplication, le chiffre 7 apparaît une fois et une seule. Ainsi, chaque étoile (*) représente un chiffre de 0 à 9 différent de 7. De plus, l'écriture d'aucun nombre ne commence par 0.
Quel en est le résultat?

Fin catégories L1 GP

15 - Le radar du Pentagone (coefficient 15)

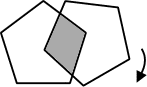
Le siège de l'état-major de l'armée des États-Unis est un bâtiment en forme de pentagone régulier, dit le Pentagone. Les services secrets viennent d'y installer un radar révolutionnaire dont la zone de détection, qui couvre également l'extérieur du bâtiment, est un pentagone identique tournant autour d'un sommet situé au centre du Pentagone. Quel est, au maximum, le pourcentage de la surface du Pentagone couvert par la zone de détection du radar, en gris sur la figure? On prendra, si besoin est, 2,236 pour √5, et on arrondira à l'entier le plus proche.

16 - Le carnet de timbres (coefficient 16)

1	2	3
5	8	17

Il est possible d'obtenir toutes les sommes entières de 1 à 36 en découpant un ou plusieurs timbres dans un carnet de timbres rectangulaire de deux timbres sur trois portant les valeurs 1, 2, 3, 5, 8 et 17, les timbres restants formant toujours un ensemble d'un seul tenant.
Pouvez-vous reconstituer ce carnet en plaçant la plus petite des quatre valeurs de coin en haut et à gauche?
L'exemple de la figure ci-dessus ne convient pas car il est impossible d'obtenir les sommes 7, 10, 12, 15, 24, 27 et 32.

Fin catégories L2 HC