15e Championnat International des Jeux Mathématiques et Logiques
demi-finale, 17 mars 2001
Catégories
- Catégorie CM (CM1, CM2): problèmes 1 à 6, 1 h 30.
- Catégorie C1 (6e, 5e): problèmes 3 à 9, 2 h.
- Catégorie C2 (4e, 3e): problèmes 5 à 11, 3 h.
- Catégorie L1 (2e, 1e, terminale): problèmes 5 à 14, 3 h.
- Catégorie GP (grand public): problèmes 5 à 14, 3 h.
- Catégorie L2 (prépa, DEUG): problèmes 5 à 16, 3 h.
- Catégorie HC (haute compétition): problèmes 5 à 16, 3 h.
(Calculatrices interdites)
Énoncés des problèmes
Début catégorie CM
- 1 - Des pommes et des poires
(coefficient 1)
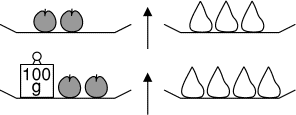
Les pommes ont toutes la même masse et les poires ont toutes la même
masse.
Quelle est la masse d'une pomme?- 2 - Les cinq dominos
(coefficient 2)
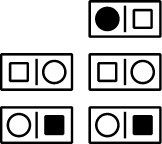
Dominique dispose des cinq dominos représentés ci-contre à droite.
Il doit les placer sur la forme ci-dessous où certains symboles des
dominos ont déjà été dessinés à la bonne place.
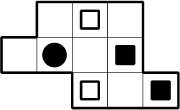
Aidez Dominique en dessinant les autres symboles.
Début catégorie C1
- 3 - Le pré Ambule
(coefficient 3)

Dédé Ambule a décidé de diviser son pré carré en cinq parcelles
rectangulaires (voir figure). Chaque parcelle a un périmètre égal
à 150 mètres.
Combien mesure le périmètre de pré Ambule?- 4 - L'imprimeur maladroit
(coefficient 4)
- Lorsque l'imprimeur a voulu numéroter les pages de ce livre, dans
l'ordre, de la page 1 à la dernière page, en ne sautant aucun nombre, il
a commis une erreur. Il a en effet tapé des
6
à la place de tous
les 9
, alors que les autres chiffres ont été tapés correctement.
La numérotation de toutes les pages a nécessité exactement 36 chiffres
6
. Quel est le nombre de pages de ce livre? Vous répondrez
en utilisant les chiffres corrects.
Début catégories C2 L1 L2 GP HC
- 5 - Les grenouilles et le prince charmant
(coefficient 5)
- Elane, Géraldine et Méline discutent sur un nénuphar:
G.: Je n'ai pas trouvé le prince
charmant
.
E.: Moi non plus, je n'ai pas trouvé
le prince charmant
.
M.: Elane ment
.
G.: Méline dit la vérité
.
Une seule des trois grenouilles ment et une seule a vraiment trouvé
le prince charmant.
Quelle est celle qui a trouvé le prince charmant?
- 6 - Escalier pas donné
(coefficient 6)

La case du haut de cet escalier contient 1 franc. On veut remplir
toutes les cases en respectant les règles suivantes.
On ne peut remplir une case que si une de ses voisines située juste
au-dessus ou immédiatement à droite contient déjà quelque chose. On peut
alors, au choix, y mettre: le double de la case située juste au-dessus,
ou bien 1 franc de plus que dans la case située immédiatement à droite,
à condition bien sûr que la case en question existe et contienne déjà
quelque chose.
Mathias a rempli toutes les cases de l'escalier en respectant les
règles du jeu. Quelle somme totale l'escalier contient-il, au
minimum?
Fin catégorie CM
Attention! Pour les problèmes 7 à 16, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 7 - L'aiguille à remonter le temps
(coefficient 7)
- Mon copain a une montre qui fonctionne bien, mais dont la trotteuse,
qui marque les secondes, tourne à l'envers, alors que les aiguilles
donnant les minutes et les heures tournent normalement. Au début de notre
devoir de maths, à 14 h pile, sa montre
indiquait l'heure exacte, sans une seconde d'erreur. Mon copain a rendu
sa copie à 14 h 45 minutes pile.
Combien de fois sa montre a-t-elle indiqué l'heure exacte pendant le
devoir (y compris au début et à la fin)?
- 8 - Le gâteau au miel
(coefficient 8)
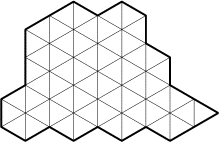
Pour son anniversaire, Mathilde a invité deux amis qui lui ont apporté
un superbe gâteau nappé de miel.
Comment peuvent-ils le découper en trois parts de même forme et de
même aire?
Note: à cause du miel, il n'est pas possible de retourner un morceau.- 9 - Les deux bandes
(coefficient 9)
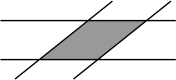
Deux bandes de papier de 1 cm de
largeur sont posées l'une sur l'autre (voir figure). La partie où deux
épaisseurs se superposent (en grisé sur le dessin) a un périmètre égal
à 8 cm.
Quelle est son aire, exprimée en
cm²? Si besoin est,
on arrondira au centième.
Fin catégorie C1
- 10 - Le livre de Al. Fa et B. Ta
(coefficient 10)
- Dans ce pays lointain, les taxes prélevées sur les ventes varient
suivant les provinces. À Algebrenbourg, toutes les ventes sont taxées
de 15%, alors qu'à Géométrieville les ventes sont taxées de 8% par le
gouvernement, puis, au prix calculé avec cette taxe, on ajoute une
seconde taxe de 5% pour obtenir le prix final.
Aliénor Fa et Bernard Ta ont acheté le même livre (donc avec le même prix
hors taxe) dans deux villes différentes.
Al. Fa l'a payé 287,5 souverains d'or à Algebrenbourg.
Combien a payé B. Ta qui a acheté son livre à
Géométrieville?
- 11 - Randonnée en montagne
(coefficient 11)
- Natacha et Véronique font de la randonnée en Gaspésie (belle région
touristique à l'est du Québec). En partant, elles ont deux sacs de même
poids. Le soir, après avoir mangé toute la nourriture qui se trouvait dans
le sac de Natacha, elles constatent que ce sac pèse alors les 2/3 du poids
de celui de Véronique (dont le contenu est inchangé depuis le départ).
Elles rééquilibrent alors les sacs pour leur donner la même masse, en
transférant uniquement des vêtements du sac de Véronique dans celui de
Natacha. Arrivées au terme de leur voyage, elles ont épuisé toutes leurs
provisions et le sac de Véronique pèse alors les 3/4 du poids de celui
de Natacha, c'est-à-dire 500 g de
moins.
Quel était le poids du sac de Véronique au départ?
Fin catégorie C2
- 12 - Le carré de l'année
(coefficient 12)
- Quel est le plus petit nombre entier positif dont le carré se
termine par les chiffres 2001?
- 13 - Un super anniversaire
(coefficient 13)
- Mathias, Mathilde et José fêtent aujourd'hui tous les trois leur
anniversaire. Ils ont des âges tous différents et Mathias, le plus jeune
des trois, a quatre ans de moins que José, le plus âgé. Férus de nombres,
ils s'amusent à calculer toutes les sommes de deux ou trois nombres
choisis parmi leurs âges. En additionnant ces sommes ils obtiennent un
premier résultat. Ils calculent ensuite toutes les différences positives
calculables entre deux de leurs âges, puis ils additionnent ces
différences et obtiennent un second résultat. Ils divisent alors le
premier résultat par le second et, surprise, ils obtiennent exactement
l'âge de José.
Quel est l'âge de José?
- 14 - La roue exploratrice
(coefficient 14)
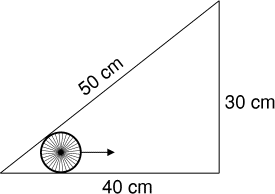
Une roue d'humeur voyageuse, et de diamètre
4 cm, décide d'explorer un
triangle de dimensions 30 cm,
40 cm et
50 cm, en roulant à l'intérieur
de celui-ci, jusqu'à revenir à son point de départ.
Quelle distance son centre aura-t-il alors parcouru?
Fin catégories L1 GP
- 15 - La clémentine de Martine
(coefficient 15)
- Martine Prey vient d'ôter la peau de sa clémentine et elle constate
que celle-ci est constituée de huit
quartiers
identiques. Le
marchand lui a affirmé que la probabilité pour que chacun des huit
quartiers contienne un ou plusieurs pépins est exactement égale à 1/3.
Quelle est la probabilité pour qu'il existe une moitié de clémentine
constituée de quatre quartiers consécutifs ne contenant aucun
pépin?
On donnera la réponse sous la forme d'une fraction irréductible.
- 16 - Mille et une lampes
(coefficient 16)
- Francis est face à une grande rangée de 1001 lampes. Initialement,
seule celle située complètement à gauche est allumée. Ensuite, toutes les
secondes, l'opération suivante est réalisée: chaque lampe change d'état si
et seulement si celle située à sa gauche était allumée une seconde avant.
La lampe située le plus à gauche reste allumée tout le temps. Le processus
s'arrête lorsque la lampe située à l'extrémité droite s'allume pour la
première fois.
Combien de lampes sont alors allumées?
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org







