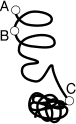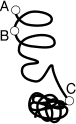16e Championnat International des Jeux Mathématiques et Logiques
1/4 de finale individuels
Date limite: 1er janvier 2002 pour la participation papier, 15 janvier 2002 pour la participation en ligne (voir le site de la FFJM). Les énoncés sont aussi parus dans Tangente n°83 (novembre-décembre 2001).
Les enseignants désireux de faire participer leurs élèves peuvent s'adresser directement à la Fédération Française des Jeux Mathématiques, 1 avenue Foch, 94700 Maisons-Alfort ou consulter le site du CIJM.
Catégories
Énoncés des problèmes
Début catégorie CE
- 1 - Les carrés
(coefficient 2)

Comptez tous les carrés de la figure ci-contre.- 2 - Le carrefour
(coefficient 1)
- Audrey arrive à un carrefour où elle peut lire les deux indications
suivantes:
Mathville 88 km
, et
Calculcity 40 km
. Quelle
est la distance entre Mathville et Calculcity, au maximum?
Début catégorie CM
- 3 - Le cube incomplet
(coefficient 3)
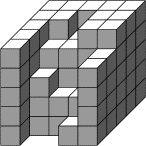
Mathias voulait construire un grand cube de 5×5×5 petits cubes. Il n'a pas
pu le terminer. Combien de petits cubes lui manquait-il?- 4 - Visite éclair au musée
(coefficient 4)
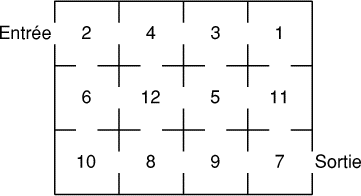
Le plan de ce musée indique le nombre de tableaux exposés dans chacune
des douze salles. Mathias n'a le temps de visiter que six salles et il
veut voir le plus grand nombre possible de tableaux. Dessinez son
trajet.
Début catégorie C1
- 5 - La tablette de Mathilde
(coefficient 5)

Mathilde a une tablette de chocolat constituée de 5 × 8 carrés.
À chaque fois qu'elle rencontre une amie, elle lui offre du chocolat en
cassant une rangée horizontale ou verticale du reste de la tablette. À
combien d'amies, au maximum, peut-elle offrir du chocolat, si elle se
garde le dernier carré?
Fin catégorie CE
- 6 - Les bougies
(coefficient 6)
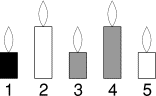
Les bougies d'Alain et de Béatrice ont la même taille. Celles de Béatrice
et de Claire ont la même couleur. Celles de Claire et Daniel n'ont pas la
même taille. Enfin, celles de Daniel et d'Alain n'ont pas la même couleur.
Quelle est la bougie d'Élodie?
Début catégories C2 L1 L2 GP HC
- 7F - La ficelle de Ludo
(coefficient 7)
[version distribuée à la finale du 15e championnat]
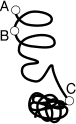
Ludo a une ficelle sur laquelle il a fait trois noeuds A, B et C. Le
morceau de ficelle AB correspond à un quinzième de la longueur totale
de la ficelle et AC à un sixième. S'il enroule le morceau AB autour
d'un tronc d'arbre, Ludo fait exactement deux tours. Combien de
tours Ludo peut-il effectuer sur le même tronc avec BC?- 7T - Le fil d'Ariane
(coefficient 7)
[version parue dans Tangente]
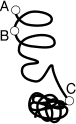
Ariane a fait trois noeuds A, B et C sur son fil téléphonique. Le morceau
AB correspond à un quinzième de la longueur totale du fil et AC à un
sixième. Si elle enroule le morceau AB autour d'un tronc d'arbre, Ariane
fait exactement deux tours. Combien de tours peut-elle effectuer sur
le même tronc avec BC?- 8 - Le plan du musée
(coefficient 8)
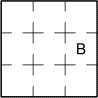
Ce musée expose dans neuf salles. La salle Braque (B) est indiquée. On
trouve des cartes postales dans la salle Ernst. De la salle Van Gogh (V),
on peut se rendre directement dans les salles Picasso (P), Cézanne (C) et
Kandinski (K). De la salle Kandinski, on peut se rendre directement dans
les salles Braque, Matisse (M) et Renoir (R). De la salle Dali (D), on ne
peut pas se rendre directement dans la salle Braque. De la salle Matisse
(M), on peut se rendre directement dans les salles Picasso et Dali.
Complétez le plan à l'aide des initiales des peintres.
Fin catégorie CM
Attention! Pour les problèmes 9 à 18, pour chaque problème
susceptible d'avoir plusieurs solutions, sur le bulletin-réponse, on
demande le nombre de solutions, et on prévoit l'emplacement pour écrire
deux solutions. Ceci ne signifie pas que ces problèmes ont toujours
plusieurs solutions. Certains peuvent n'avoir qu'une seule solution!
- 9 - Février palindrome
(coefficient 9)
- On écrit les dates sous la forme
jjmmaaaa
(par exemple
01092001 pour le 1er septembre 2001). Le 20 février 2002
s'écrira 20022002. Un tel nombre, qui se lit de la même façon de
gauche à droite et de droite à gauche, est un nombre palindrome.
Quelle sera la date palindrome suivante?
- 10 - Les maisons amies
(coefficient 10)
- Ma rue comprend exactement 99 maisons numérotées de 1 à 99, les
numéros pairs étant situés d'un côté et les impairs de l'autre. Il se
trouve que lorsque deux maisons sont numérotées à l'aide de numéros à
deux chiffres utilisant les deux mêmes chiffres dans un ordre différent,
et que la différence entre les deux numéros (le plus grand moins le plus
petit) est égale à 45, alors les familles qui habitent ces maisons sont
amies. Combien y a-t-il de paires de familles amies dans ma rue, au
minimum?
- 11 - Bon pour un 421
(coefficient 11)
[version parue dans Tangente]
- Mathias et Mathilde jouent au jeu suivant. Ils ont écrit, dans
cet ordre, les neuf chiffres 1 2 3 4 5 6 7 8 9 et ils essaient, en
intercalant entre certains chiffres, une ou plusieurs fois, un ou
plusieurs des symboles +, -, × et /, d'obtenir 421.
Mathilde a écrit 1+2×3-45+6×78-9=421, tandis que Mathias a trouvé
12×34-56+78-9=421.
Proposez-leur une autre solution.
Fin catégorie C1
- 12 - La cible
(coefficient 12)

Dans cette cible, le cercle moyen a un rayon double de celui du petit et
le grand cercle a un rayon triple de celui du petit cercle. La cible a une
aire totale égale à 1113 cm².
Quelle est l'aire de la zone blanche? On pourra prendre 22/7 pour
π.- 13F - Le parallélogramme
(coefficient 13)
[version distribuée à la finale du 15e championnat]
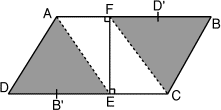
Mathias a devant lui un parallélogramme de papier. Il le plie selon un
segment [AE] de telle sorte que D vienne en D', puis le déplie et le plie
à nouveau selon [CF] de telle sorte que B vienne en B'. On constate alors
que (EF) est perpendiculaire aux côtés [AB] et [DC]. De plus, on sait que
AD = 10 cm et
AF = 5 cm. Quelle est
l'aire du parallélogramme? On pourra prendre, si besoin est, 1,414
pour √2; 1,732 pour √3 et 3,14 pour π, et on arrondira
si besoin est au mm² le plus
proche.- 13T - Le parallélogramme
(coefficient 13)
[version parue dans Tangente]

Mathias a devant lui un parallélogramme de papier. Il le plie selon un
segment [AE] de telle sorte que D vienne en D', puis le déplie et le plie
à nouveau selon [CF] de telle sorte que B vienne en B'. On constate alors
que (EF) est perpendiculaire aux côtés [AB] et [DC]. De plus, on sait que
AD = 10 cm et
AF = 5 cm. Quelle est
l'aire du parallélogramme?
On pourra prendre, si besoin est, √2 = 1,414;
√3 = 1,732 et π = 3,14. On arrondira
si besoin est au cm² le plus
proche.
Fin catégorie C2
- 14 - Rectangle de hasard
(coefficient 14)
- Je lance deux dés à six faces, numérotées de 1 à 6. Les
deux nombres obtenus sont la longueur et la largeur (en
cm) d'un rectangle que je construis.
Je m'aperçois alors qu'en augmentant d'un même nombre entier de
cm la longueur et la largeur
de ce rectangle, son aire double. Quelle est l'aire, en
cm², du rectangle
doublé?
- 15 - Le vélo sans chaîne
(coefficient 15)
[version parue dans Tangente]
- Léa a trouvé un petit vélo auquel il manque la chaîne. Le grand
pédalier denté a un rayon de 21 cm
et la petite roue dentée un rayon de
3 cm, la distance entre les deux
centres étant de 36 cm. Quelle
est, au minimum, la longueur de la chaîne que Léa doit acheter? On
prendra 3,1416 pour π et 1,732 pour √3. On arrondira au
mm le plus proche.
- 16 - Le retour de Pent'X
(coefficient 16)
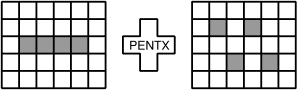
Pour que Pent'X puisse loger dans une maison, on doit pouvoir l'y poser
de telle façon que ses contours coïncident avec les contours des petits
carrés de la maison, sans qu'il recouvre un petit carré grisé.
Il suffit de griser 4 cases d'une grille à 5 lignes et 6 colonnes pour
qu'elle devienne inhabitable
par Pent'X, comme le rappellent les
deux exemples ci-dessus.
Mais combien existe-t-il de façons différentes (y compris les deux
précédentes) de griser ainsi 4 cases pour que la grille devienne
inhabitable par Pent'X? Des grilles identiques par symétrie ou
retournement seront comptées pour une seule.
Fin catégories L1 GP
- 17 - Le polygone mystérieux
(coefficient 17)
- Ludo vient de calculer le côté d'un polygone régulier à
douze côtés (un dodécagone) inscrit dans un cercle de rayon
1 cm. Il a trouvé
√(2 - √3) cm.
Papy Georges, qui passait par là, lui indique qu'un polygone régulier
inscrit dans le même cercle a un côté mesurant, en
cm:
√(2-√(2+√(2+√(2+√3)))).
Combien ce polygone compte-t-il de côtés?
- 18 - Le terrain du père C. Cussion
(coefficient 18)
- Charles Cussion possède un terrain triangulaire sur lequel se
trouve une mare parfaitement circulaire et tangente aux trois côtés
du terrain, de diamètre 42 m. Charles
clôt entièrement son terrain et remarque qu'un des points de tangence
de la mare partage le côté correspondant du triangle en deux segments
de longueurs respectives 23 m et
27 m. Quelle est la longueur totale
de la clôture du terrain du père C. Cussion? On donnera une
réponse éventuellement arrondie au cm
le plus proche.
Fin catégories L2 HC
Dernière modification: 30 mars 2002
webmaster@vinc17.org